Question

What is the total surface area of a cone if its radius = 5cm and height = $\sqrt 2 $cm?
$
  A.{\text{ 159}}{\text{.983m}}{{\text{m}}^2} \\
  B.{\text{ 159}}{\text{.983c}}{{\text{m}}^2} \\
  C.{\text{ 159}}{\text{.983cm}} \\
  D.{\text{ 159}}{\text{.983}}{{\text{m}}^2} \\
$

Answer 1

Hint: We can find the total surface of cone by simple formula for total surface area of cone $ = \pi rl + \pi {r^2}$ where $r$is radius of cone and $l$is slant height of a cone and slant height $l = \sqrt {{h^2} + {r^2}} $.

Complete step-by-step answer:

Where h and r are height and radius respectively.

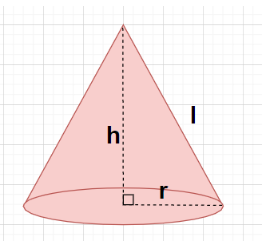
It is given in the question the height of cone $ = \sqrt 2 cm$
And the radius of cone $ = 3cm$
Then by using the formula, slant height
  $
   = \sqrt {{h^2} + {l^2}} \\
   = \sqrt {{{\sqrt 2 }^2} + {5^2}} \\
   = \sqrt {2 + 25} \\
   = \sqrt {27} \\
   = 5.19cm \\\
$
Now. Total Surface area of cone $ = \pi r(l + r)$
$
   = 3.14 \times 5 \times (5 + 5.19) \\
   = 3.14 \times 5 \times 10.19 \\
   = 159.983c{m^2} \\
$

Note: Whenever we are stuck with this type of question, we simply have to check first what are the parameters given of a particular object then check what parameter is missing then after finding or calculating that parameter use the formula and then find the total surface area of the cone.