Question

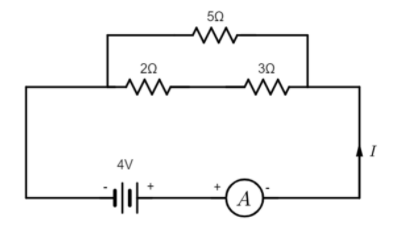
What is the total resistance and current in the circuit?

A. $2.5\Omega$, $0.4\;A$
B. $2\Omega$, $1.6\;A$
C. $2.5\Omega$, $1.6\;A$
D. $6\Omega$, $1.6\;A$

Answer 1

Hint: First find the net resistance for the two resistors in series by summing them up. Then find the effective resistance between the parallel branches of the resistors. This will be the total resistance offered by the circuit. To this end, given a voltage of 4V, use the Ohm’s Law to obtain the total current flowing through the circuit.
Formula Used:
Effective resistance of two resistors in series: $R_{eff} = R_1 +R_2$
Effective resistance of two resistors in parallel: $R_{eff} = \dfrac{R_1 R_2}{R_1 +R_2}$
Ohm’s law for current flowing through a resistor: $I=\dfrac{V}{R}$

Complete answer:
The circuit diagram suggests that there are multiple resistances in the circuit, in series and in parallel, and we must first find the effective resistance of the circuit. This is because the voltage drops across the series resistances are different, and the currents flowing through the parallel branches of resistances are different.
We see that the $2\Omega$ and the $3\Omega$ resistors are in series with each other, and they together, are in turn, in parallel with the $5\Omega$ resistor. So, we have to calculate the effective resistance of the circuit accordingly.
For the two series resistances, effective resistance is $2+3=5\Omega$
Now this effective resistance is in parallel with the $5\Omega$ resistance. The net resistance of the circuit will thus be:
$R_{net} = \dfrac{5 \times 5}{5 + 5} = 2.5\Omega$
Given that the voltage across the circuit is $4V$, the current through the circuit can be found by using Ohm’s Law:
$V= IR \Rightarrow I = \dfrac{V}{R_{net}} = \dfrac{4}{2.5} = 1.6\;A$

Therefore, the correct choice would be: C. $2.5\Omega$, $1.6\;A$.

Note:
Remember that a series circuit is a voltage divider whereas a parallel circuit is a current divider. We add up all the resistances in a series circuit because the resistances are arranged in such a way that the current has only one path to take. However, when resistances are connected in parallel, there are multiple paths for the current to pass through but have the same potential difference across them. This results in a net resistance that is lower than any of the individual resistances.