Question

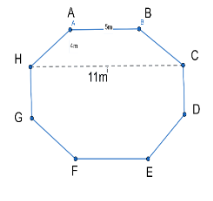
Top surface of a raised platform is in the shape of a regular octagon as shown in the figure. Find the area of the octagonal surface.

Answer 1

Hint:We have to find the area of the octagonal surface. So for that you should know the area of two trapezium and rectangle. So the area of the octagonal surface will be $2$(Area of trapezium $ABCH$)$+$Area of rectangle $HCDG$. Try it, you will get the answer.

Complete step-by-step answer:

We have to find the area of the octagonal surface.
 Area of octagonal surface= Area of trapezium $ABCH$$+$Area of rectangle $HCDG$$+$Area of trapezium $GDEF$
So in short,
Area of octagonal surface= $2$(Area of trapezium $ABCH$)$+$Area of rectangle $HCDG$ …………..(1)
Here all sides are equal to $5m$ .
So now the area of trapezium $ABCH$$=$$\dfrac{1}{2}\times $(Sum of parallel sides)$\times $height.
$AB$ and $HC$ are parallel sides.
$AB=5m$ and $HC=11m$
Area of trapezium$=\dfrac{1}{2}\times (11+5)\times 4=32{{m}^{2}}$ ………. (2)
Now area of rectangle$HCDG$$=$length $\times $breadth.
length$=HC=11m$
breadth$=CD=5m$
area of rectangle$HCDG$$=11\times 5=55{{m}^{2}}$ …………(3)
Now from (1), (2) and (3), we get,
Area of octagonal surface$=2(32)+55=64+55=119{{m}^{2}}$
So we get the area of octagonal surface is $119{{m}^{2}}$.

Note: Read the question carefully. Your concept regarding menstruation should be clear. Also, do not make silly mistakes. While solving, take care that no terms are missed. You should know the area of all.