Question

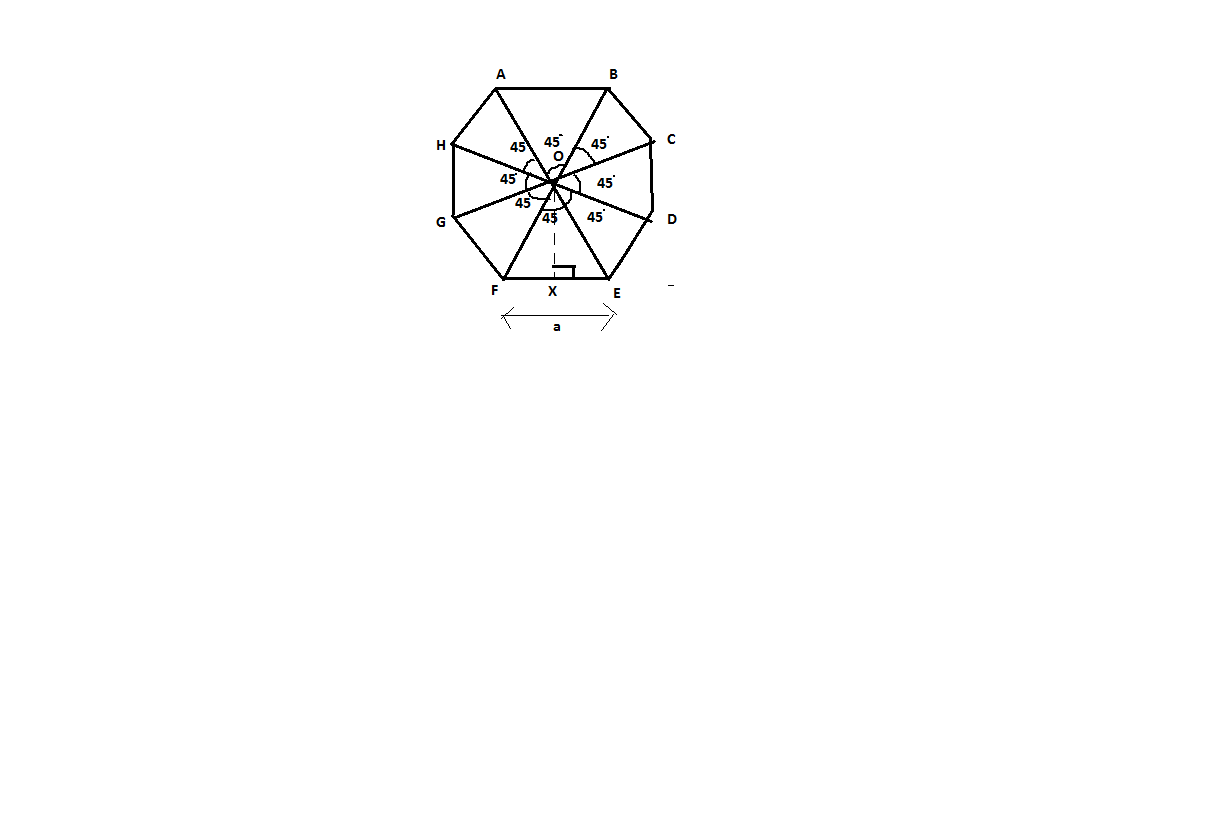
Top surface of a raised platform is in the shape of a regular octagon as shown in figure. Find the area of the octagonal surface.

Answer 1

Hint:
For finding the area of a regular octagon, properties of a regular octagon must be known.
Properties: 1. All the sides are of equal length.
2. Sum of all exterior angles of a regular octagon is ${360^ \circ }$
3. Sum of all interior angles of a regular octagon is ${1080^ \circ }$

Complete step by step solution:
 Here below is a figure of regular octagon ABCDEF, where each side is of ‘a’ length

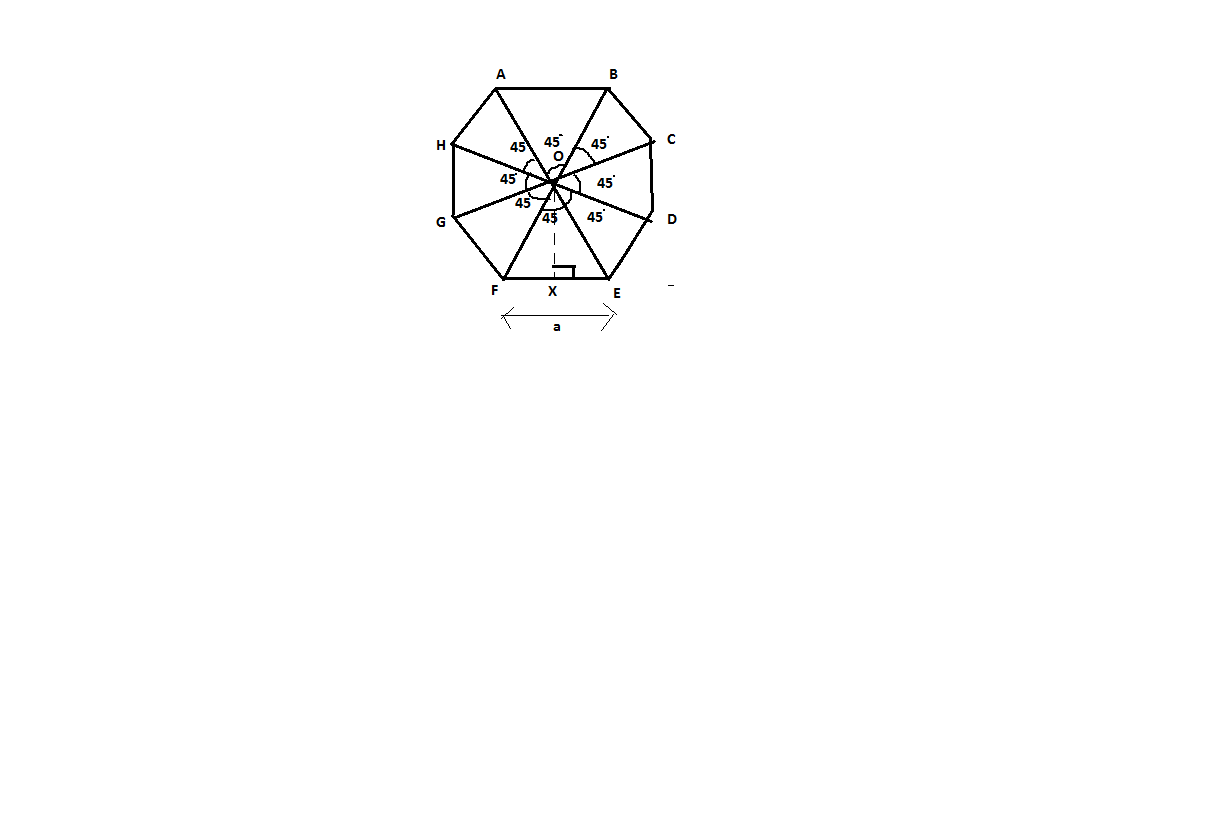
This view is from above the surface so we will take the exterior angle sum which is 360˚. To find angle subtended by each side we will simply divide the total angle into 8 parts.
Angle subtended at the centre $ = \dfrac{{{{360}^ \circ }}}{{{8^ \circ }}} = {45^ \circ }$
Now for finding the area we must find area of one triangle and by which we can simply find the area of whole octagon ,for this take a section of a triangle shown below and just dram a perpendicular bisector OX on line FE ($OX \bot FE$ )

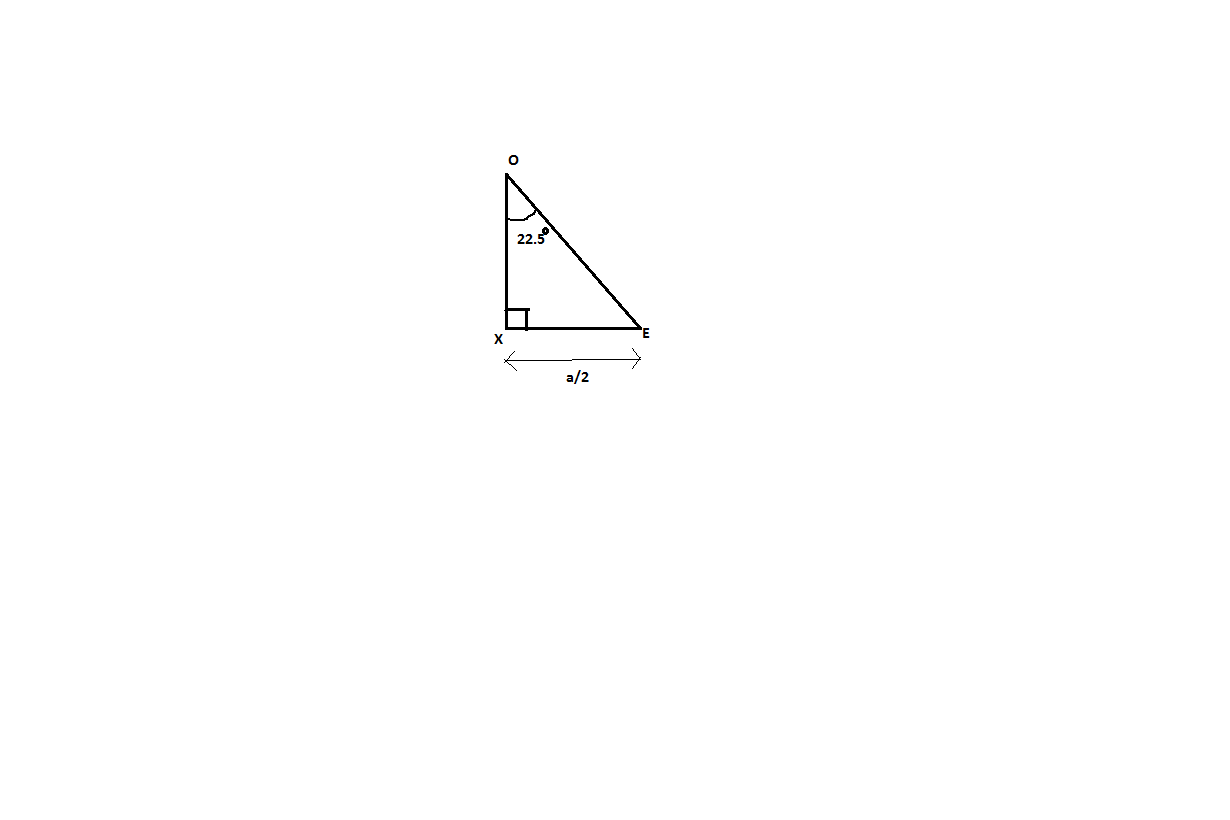
Perpendicular bisector divides the angle and side into two equal parts.
$\therefore $ $\angle XOE = \dfrac{{{{45}^ \circ }}}{2} = {22.5^ \circ }$
 $\therefore FX = XE = \dfrac{a}{2}cm$
Now in applying the trigonometric function and finding height.
$\tan 22.5 = \dfrac{p}{b} = \dfrac{{EX}}{{OX}} = \dfrac{{a \div 2}}{{OX}}.................(1)$
Putting the value of $\tan {22.5^ \circ } = 0.4142$ in equation 1.
$\therefore \dfrac{{a \div 2}}{{OX}} = 0.4142$
By cross multiplying we will get $OX = \dfrac{a}{{2 \times 0.414}} = \dfrac{a}{{0.828}}cm$
Now in ,
area of
$ = \dfrac{1}{2} \times a \times \dfrac{a}{{0.828}} = \dfrac{{{a^2}}}{{1.656}}c{m^2}$

Area of regular octagon $ = 4.82{a^2}c{m^2}$

Note:
We can solve this question by another method which is as follows: -

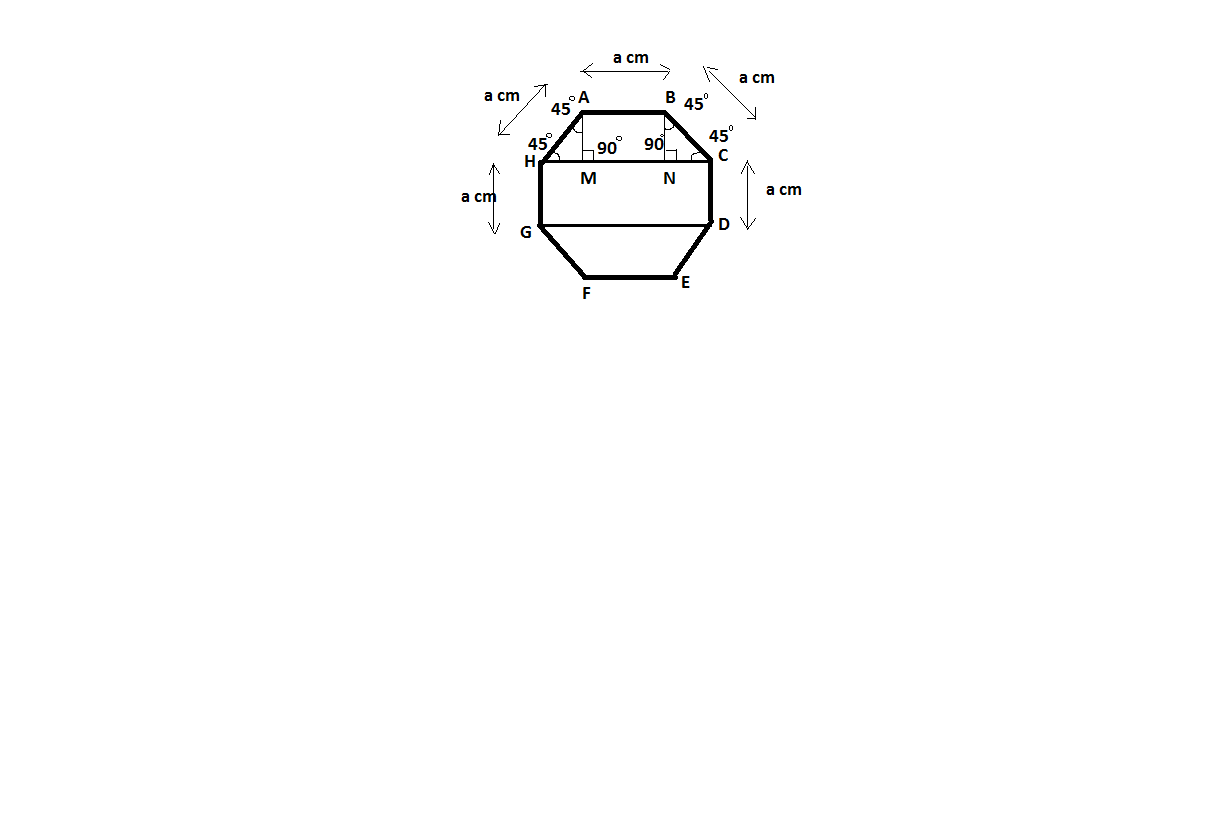
Alternate method: -
Construction: - Join points HC and GD which will result into a trapezium ABCNMH having two perpendicular heights AM and BM.
We can see in the above figure that in trapezium ABCNMH there are two triangles and one rectangle so we can easily find out the area of triangles and rectangle and then add them, similarly below trapezium GDEF’s area can also be found out. In the middle there is a rectangle HCDG whose area can also be found out. Adding all the areas will result in a net area of a regular octagon.
Step by step solution: -
In triangle AHM
$\sin \theta = \dfrac{p}{h} = \dfrac{{AM}}{{AH}}$
$ \Rightarrow \sin \theta = \dfrac{{AM}}{a}$
$ \Rightarrow \sin {45^ \circ } = \dfrac{{AM}}{a}$
$ \Rightarrow AM = \sin {45^ \circ } \times a$
$\therefore AM = \dfrac{a}{{\sqrt 2 }}cm$
In triangle HAM
$\cos \theta = \dfrac{b}{h} = \dfrac{{HM}}{{AH}}$
$ \Rightarrow \cos \theta = \dfrac{{HM}}{a}$
$ \Rightarrow \cos {45^ \circ } = \dfrac{{HM}}{a}$
$ \Rightarrow HM = \sin {45^ \circ } \times a$
$\therefore HM = \dfrac{a}{{\sqrt 2 }}cm$
Area of triangle AMH=$\dfrac{1}{2} \times b \times h$
$ \Rightarrow \dfrac{1}{2} \times HM \times AM$
$ \Rightarrow \dfrac{1}{2} \times \dfrac{a}{{\sqrt 2 }} \times \dfrac{a}{{\sqrt 2 }}$
$ \Rightarrow \dfrac{1}{2} \times \dfrac{{{a^2}}}{{{{(\sqrt 2 )}^2}}}$
$ \Rightarrow \dfrac{1}{2} \times \dfrac{{{a^2}}}{2} = \dfrac{{{a^2}}}{4}c{m^2}$
$\therefore $Area of triangle AMH=$\dfrac{{{a^2}}}{4}c{m^2}$
Similarly BN and NC and area of triangle BNC can also be find out.
 $\therefore BN = \dfrac{a}{{\sqrt 2 }}cm$
$\therefore NC = \dfrac{a}{{\sqrt 2 }}cm$
$\therefore $Area of triangle BNC=$\dfrac{{{a^2}}}{4}c{m^2}$
In rectangle ABNM
Area of rectangle ABNM =$MN \times BN$
$ \Rightarrow a \times \dfrac{a}{{\sqrt 2 }}$
$ \Rightarrow \dfrac{{{a^2}}}{{\sqrt 2 }}c{m^2}$
Area of trapezium ABCNMH= area of two triangles (AMH and BNC) +area of rectangle ABNM
$ \Rightarrow \dfrac{{{a^2}}}{4} + \dfrac{{{a^2}}}{4} + \dfrac{{{a^2}}}{{\sqrt 2 }}$
$ \Rightarrow \dfrac{{{a^2} + {a^2}}}{4} + \dfrac{{{a^2}}}{{\sqrt 2 }}$ (Taking LCM of first two terms)
$ \Rightarrow \dfrac{{2{a^2}}}{4} + \dfrac{{{a^2}}}{{\sqrt 2 }}$
$ \Rightarrow {a^2}(\dfrac{1}{2} + \dfrac{1}{{\sqrt 2 }} \times \dfrac{{\sqrt 2 }}{{\sqrt 2 }})$ (Rationalising $\sqrt 2 $ )
$ \Rightarrow {a^2}(\dfrac{1}{2} + \dfrac{{\sqrt 2 }}{2})$
$ \Rightarrow {a^2}(\dfrac{{1 + \sqrt 2 }}{2})$
$\therefore $Area of trapezium ABCNMH=${a^2}(\dfrac{{1 + \sqrt 2 }}{2})c{m^2}$
Similarly, area of trapezium GDEF=${a^2}(\dfrac{{1 + \sqrt 2 }}{2})c{m^2}$
In rectangle HCDG
Area of rectangle HCDG=$l \times b$=$CD \times HC$
CD=a cm
HC=HM+MN+NC=$\dfrac{a}{{\sqrt 2 }} + a + \dfrac{a}{{\sqrt 2 }}$
$ \Rightarrow \dfrac{{a + a}}{{\sqrt 2 }} + a = \dfrac{{2a}}{{\sqrt 2 }} + a$ (Taking LCM of first two terms)
$ \Rightarrow \dfrac{{2a}}{{\sqrt 2 }} \times \dfrac{{\sqrt 2 }}{{\sqrt 2 }} + a$ (Rationalising$\sqrt 2 $)
$ \Rightarrow \sqrt 2 a + a = a(\sqrt 2 + 1)cm$
 (Multiplying$\sqrt 2 $with$\sqrt 2 $which will give 2 and then cancelling with numerator 2)
$\therefore $HC=$a(\sqrt 2 + 1)cm$
$\therefore $Area of rectangle HCDG=$a(\sqrt 2 + 1) \times a = {a^2}(\sqrt 2 + 1)c{m^2}$
Area of regular octagon=area of both trapezium (ABCNMH+GDEF) +area of rectangle (HCDG)
$ \Rightarrow {a^2}(\dfrac{{1 + \sqrt 2 }}{2}) + {a^2}(\dfrac{{1 + \sqrt 2 }}{2}) + {a^2}(\sqrt 2 + 1)$ (Adding first two similar terms)
$ \Rightarrow {a^2}(\sqrt 2 + 1) + {a^2}(\sqrt 2 + 1)$ (Adding similar terms)
$ \Rightarrow 2{a^2}(\sqrt 2 + 1)$
$ \Rightarrow 2{a^2}(1.414 + 1)$ (=1.414)
\[ \Rightarrow 2{a^2}(2.414) = 4.828{a^2}c{m^2}\]
\[\therefore 4.828{a^2}c{m^2}\]