Question

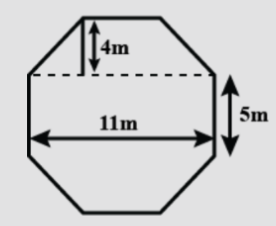
Top surface of a raised platform is in the shape of a regular octagon as shown in the figure. Find the area of the octagonal surface.

Answer 1

HINT: The given figure can be divided into 2 similar trapeziums and 1 rectangle.
The area of a trapezium is given by the formula
Area \[=\dfrac{h\cdot ({{l}_{1}}+{{l}_{2}})}{2}\] (Where ‘h’ is the height between the two parallel faces of a trapezium and \[{{l}_{1}}\ and\ {{l}_{2}}\] are the lengths of the parallel sides)
The area of a rectangle is given by the formula
Area \[=l\times b\] (Where ‘l’ is the length of the rectangle and ‘b’ is the breadth of the rectangle).

Complete step by step answer:
As given in the question, the value of the length of one of the parallel sides of the trapezium is 11 m and the height of the trapezium is 4 m.
As the figure is a regular octagon, therefore, we can get the length of the other parallel side as 5 m.
Now, the area of the trapezium is
\[\begin{align}
  & =\dfrac{4\times (11+5)}{2} \\
 & =4\times 8 \\
 & =32\ {{m}^{2}} \\
\end{align}\]
(Using the formula as mentioned in the hint) \[\]
 Similarly, the area of the rectangle can be calculated as its length and breadth are 11 m and 5 m respectively.
\[\begin{align}
  & =11\times 5 \\
 & =55\ {{m}^{2}} \\
\end{align}\]
Hence, the area of the complete octagon is area of rectangle+ \[2\times \] area of trapezium.
Therefore, the area is 55+ \[2\times \] 32 that is \[119\ {{m}^{2}}\] .

NOTE:The students can make an error in finding the plane or line of symmetry in the octagon but that is of no use.Every figure’s area can be evaluated similarly, just by dividing the figure into smaller and simpler shapes.

.