Question

To mop-clean a floor, a cleaning machine presses a circular mop of radius R vertically down with a force F and rotates it with a constant angular speed about its axis. If the force F is distributed uniformly over the mop and if the coefficient of friction between the mop and the floor is $\mu $, the torque, applied by the machine on the mop is:
\[\begin{align}
  & A.~~~~~~~~~\dfrac{2\mu FR}{3} \\
 & B.~~~~~~~~~\dfrac{\mu FR}{3} \\
 & C.~~~~~~~~~\dfrac{\mu FR}{2} \\
 & D.~~~~~~~~~\dfrac{\mu FR}{6} \\
\end{align}\]

Answer 1

Hint: As the mop is rotating with constant angular speed, the net torque on it must be zero. To find the torque of the force applied by the machine, we can find the torque of all other forces and make the sum of all torques equal to zero.

Complete step by step answer:
 The machine applies a force F and also applies a torque. The force F is applied vertically downward; this force will be completely balanced by normal (as the acceleration of mop is zero along vertical). So,
\[N=F\] ……………………………………………………….. (1),
Where N is normal from the floor.
Now, we are given that mop rotates with a constant angular velocity which means the net torque on it is zero.
${{\tau }_{m}}+{{\tau }_{f}}+{{\tau }_{N}}+{{\tau }_{F}}=0$
Since the force F and normal N are exactly equal and opposite, also they are acting uniformly over the mop. So we can write
 ${{\tau }_{N}}+{{\tau }_{F}}=0$
From the above relation, we can say that
${{\tau }_{m}}+{{\tau }_{f}}=0$
So, the torque due to the machine can be calculated by calculating torque due to friction.
The total magnitude of friction will be
$f=\mu N$,
Where $\mu $ is the coefficient of friction between the mop and the floor
Using the value of N from equation 1, we can write
$f=\mu F$
To find the torque due to friction, we will take a ring at distance r from the mop

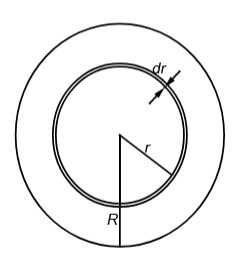
Friction acting on this small section can be written as
${{\tau }_{df}}=-\dfrac{\mu N}{\pi {{R}^{2}}}\times 2\pi rdr$ , friction per unit area multiplied by the area of the ring (product of length and thickness)
To find the total magnitude of torque we can integrate it with limits from zero to R
${{\tau }_{f}}=\int\limits_{0}^{R}{-\dfrac{\mu N}{\pi {{R}^{2}}}\times 2\pi rdr}=~-\dfrac{2\mu FR}{3}$
The torque of force due to the machine will be negative of it. Therefore,
 ${{\tau }_{m}}=\dfrac{2\mu FR}{3}$
Hence the correct option is A.
Note: The torque of normal and force f will cancel each out because both are being applied at equal distances from the axis and both of them have the same magnitude and opposite direction too. The torque of a force from an axis is equal to the product of the magnitude of the force and the perpendicular distance of force from the axis.