Question

To locate the position of an object or a point in a plane, we require two perpendicular lines. One is horizontal and the other is vertical.
(a) True
(b) False.

Answer 1

Hint: We solve this problem by using the general co – ordinate axes. We have the co – ordinate axes in a 2D plane as follows.

By using this co – ordinate axes we can locate the point in the plane as co – ordinates.
Then we check whether for some other lines also whether we can locate the point or not.

Complete step-by-step answer:
We know that for the location of a point or an object we use the co – ordinate axes.
Let us assume that there is a point \[P\left( x,y \right)\] in the co – ordinate plane.
We know that the value of \['x'\] is the perpendicular distance from point to vertical axis.
We also know that the value of \['y'\] is the perpendicular distance from point to horizontal axis.
Let us plot this point in the figure then we get

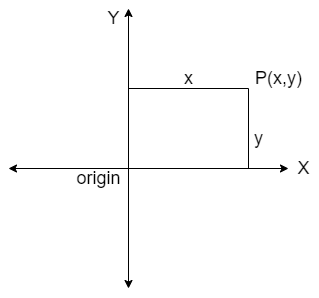
Here, we can see that the X – axis is horizontal line and the Y – axis is vertical line.
So, we can say that we need two lines to locate a point.
Now, let us rotate the axes through an angle \['\theta '\] in anti – clockwise direction then we get

Here, we can see that the old transformed axes XY are transformed to new axes AB.
Here, we can see that we can locate the point P in the new axes by using the transformation of axes.
So, we get the new co – ordinates with respect to axes AB as \[P\left( a,b \right)\]
We have the formula for finding the values of \[a,b\] as
\[\begin{align}
  & \Rightarrow a=x\cos \theta +y\sin \theta \\
 & \Rightarrow b=-x\sin \theta +y\cos \theta \\
\end{align}\]
Here, we can see that the axis ‘A’ is not horizontal and axis ‘B’ is not vertical.
But we are finding the new co – ordinates by using the old co – ordinates. This means that we are depending on the old co – ordinates which are perpendicular lines in which one is horizontal and other is vertical. So, however we rotate the axes, the two perpendicular lines required to locate the point in that axes are horizontal and vertical.
So, we can conclude that the given statement that is to locate the position of an object or a point in a plane, we require two perpendicular lines in which one is horizontal and the other is vertical is correct.

So, the correct answer is “Option (a)”.

Note: Students may make mistakes in taking all the theories. We have the general coordinate axes which are horizontal and vertical lines. But when we rotate the axes through an angle \[\theta \] then also we can locate the point in that coordinate axes which are not horizontal and vertical lines.
Here, we can see that the new and old co-ordinate axes are perpendicular to each other but they need not be vertical and horizontal. But, without the old co – ordinate axes we cannot find the point in the new co – ordinate axes. So, the given statement should be correct because we are mainly depending on the new axes in which the lines are perpendicular and one is vertical and the other is horizontal. Students may miss this condition and assume that the given statement is incorrect.