Question

To get from one office to another, one travels as follows (with all angles measured clockwise from the west) $2m$ at $180{}^\circ $, $0.5m$ at $150{}^\circ $, and $1m$ at $30{}^\circ $. How far will a person be from his starting point? (in m)
   $\begin{align}
  & A)1.5m \\
 & B)1.74m \\
 & C)1m \\
 & D)1.96m \\
\end{align}$

Answer 1

Hint: For finding the distance of the person from the starting point, we have to take distances travelled in each direction by the person in vector form. Then we will draw a diagram by taking x-axis as east-west and y-axis as North West. After finding the final point of the person, we will take the difference in distance from his starting point which will give us the answer.

Complete answer:
Initially, let us draw a diagram by taking x-axis as east-west and y-axis as North West. Here, +x- axis is taken as east, -x-axis is taken as west, +y-axis is taken as north and –y-axis is taken as south.
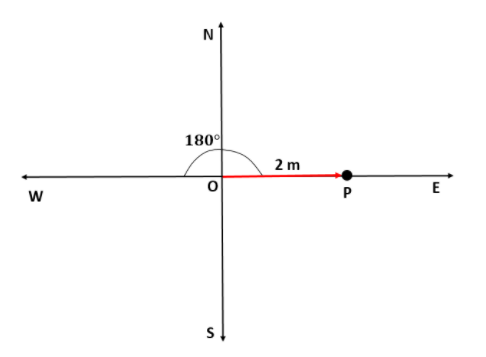
Now, let us assume that the person's starting point is O, which is the origin and he was moving $2m$ at $180{}^\circ $ from west. That is, he will be moving in the east direction. Let that point be P.
 

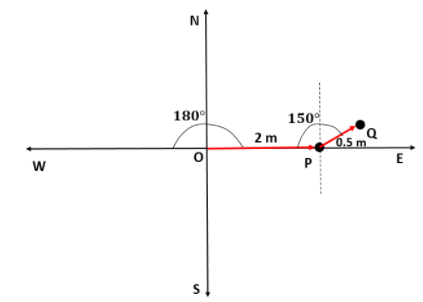
Now, the person is at P and moves $0.5m$ at $150{}^\circ $ from his west. So, he will be moving in the north-east direction. Let that point be Q.
             

Now, the person is at Q and moves $1m$ at $30{}^\circ $ from his west. So, he will be moving in the north-west direction. Let that point be R.
            

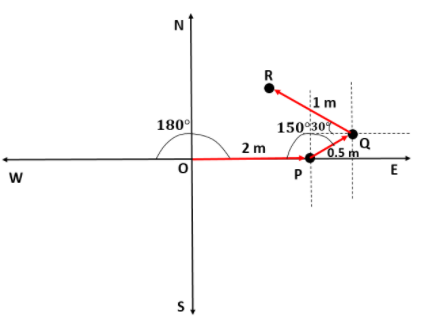
Now, we will find the coordinates of R.
Distance travelled in +x direction = $2\widehat{i}$
Distance moved in north-east direction = $0.5\cos \left( 30{}^\circ \right)\widehat{i}+0.5\sin \left( 30{}^\circ \right)\widehat{j}$
Since, $180{}^\circ -150{}^\circ =30{}^\circ $
Distance moved in north-west direction = $1\sin \left( 60{}^\circ \right)\widehat{i}+1\cos \left( 60{}^\circ \right)\widehat{j}$
Since, the person is moving towards –x direction and +y direction and we are taking the angle in clockwise direction.
Now, the coordinates of final position (R) of the person will be,
\[\begin{align}
  & R\left( x,y \right)=\left( 2+0.5\cos \left( 30 \right)-1sin\left( 60 \right) \right)\widehat{i}+\left( 0.5\sin \left( 30 \right)+1\cos \left( 60 \right) \right)\widehat{j} \\
 & \Rightarrow R\left( x,y \right)=\left( 2+\dfrac{\sqrt{3}}{4}-\dfrac{\sqrt{3}}{2} \right)\widehat{i}+\left( \dfrac{1}{4}+\dfrac{1}{2} \right)\widehat{j} \\
 & \Rightarrow R\left( x,y \right)=\left( 2-\dfrac{\sqrt{3}}{4} \right)\widehat{i}+\left( \dfrac{3}{4} \right)\widehat{j} \\
 & \Rightarrow R\left( x,y \right)=\left( \dfrac{8-1.732}{4} \right)\widehat{i}+\left( \dfrac{3}{4} \right)\widehat{j}\text{ }\left( \because \sqrt{3}=1.7320 \right) \\
 & \therefore R\left( x,y \right)=\left( 1.567 \right)\widehat{i}+\left( 0.75 \right)\widehat{j} \\
\end{align}\]
Now, the distance of the person from his starting position will be the hypotenuse of the triangle.
That is,
$\begin{align}
  & O{{R}^{2}}={{x}^{2}}+{{y}^{2}} \\
 & \Rightarrow O{{R}^{2}}={{\left( 1.567 \right)}^{2}}+{{\left( 0.75 \right)}^{2}} \\
 & \Rightarrow O{{R}^{2}}=2.455489+0.5625 \\
 & \Rightarrow O{{R}^{2}}\approx 3.016 \\
 & \Rightarrow OR=\sqrt{3.016} \\
 & \therefore OR=1.74m \\
\end{align}$
So, the person is $1.74m$ far from his starting point.

Therefore, option B is correct.

Note:
For solving this type of question, drawing a diagram is a must. Also, try to measure the angle in only one direction throughout the solution. Be precise with calculations. While taking components of a vector, take the adjacent component to the angle as cos and the other as sine.