Question

To draw parallel lines we use, $$$$
A. Compass $$$$
B. Divider $$$$
C. Scale and set squares $$$$
D. Scale and protractor $$$$

Answer 1

Hint: We recall the definition uses of scale, divider, compass, protractor and set squares. We recall the definitions of parallel lines and demonstrate how we can use edges of set squares to draw a parallel line of $\overleftrightarrow{AB}$ passing through a point P. $$$$

Complete step-by-step solution
We know that in our geometry box different types of instruments are used. The scale or ruler is an instrument used to measure the length in cm or inch of distance between two points and also to draw straight lines. A divider otherwise known as a compass is used to locate points while a compass is used to draw arc and circle. A protractor is an instrument to measure angles with the unit degree. $$$$
The set squares are a type of drawing instrument whose two edges are perpendicular to each other. There are two types of set squares. The smaller one is ${45}^{\circ }-{45}^{\circ }$ set square whose edges of equal length and both the acute angles are of measure ${45}^{\circ }$.The larger one is ${30}^{\circ }-{60}^{\circ }$ set square whose edges are not of equal length and the acute angles are of measure ${30}^{\circ },{60}^{\circ }$. $$$$
Parallel lines are two straight lines that never intersect each other. We draw the rough figure of two straight lines $\overleftrightarrow{AB},\overleftrightarrow{PQ}$ which are parallel below .$$$$
We draw parallel lines with the help of a scale and set squares, for that we first draw the line $\overleftrightarrow{AB}$ with a scale and locate the point P. $$$$

We align the hypotenuse of ${45}^{\circ }-{45}^{\circ }$ set square (shown in red colour below)with it and then align ${30}^{\circ }-{60}^{\circ }$ set square with the side of ${45}^{\circ }-{45}^{\circ }$ show in green colour below. $$$$

We fix the ${30}^{\circ }-{60}^{\circ }$ with our left hand and move the ${45}^{\circ }-{45}^{\circ }$ set square so that the hypotenuse passes through P. $$$$

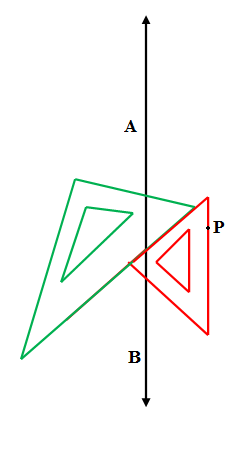
We use to draw the line through P and extend with a scale to get the parallel line of $\overleftrightarrow{AB}$ passing through P as $\overleftrightarrow{PQ}$$$$$

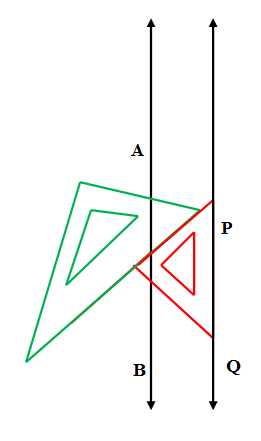
So the correct option is C.

Note: We note that the distance between two parallel lines is always equal. This method of drawing parallel lines is also used to construct trapezium. If the lines are not parallel then they are intersecting. We can also draw parallel lines using scale and compass taking arcs of equal width.