Question

To draw a pair of tangents to a circle which are inclined to each other at an angle of ${{60}^{\circ }}$, it is required to draw tangents at end points of those two radii of the circle, the angle between them should be :
A. ${{100}^{\circ }}$
B. ${{140}^{\circ }}$
C. ${{120}^{\circ }}$
D. ${{135}^{\circ }}$

Answer 1

Hint: Draw a rough diagram of a circle with a pair of tangents to the circle drawn from a single point. Join the radius at the points of contact of the tangent with the circle. Assume the angle between the two radii as $\theta $. Apply the property of quadrilateral, that, ‘sum of all interior angles is equal to ${{360}^{\circ }}$’ and find the value of $\theta $. Use the theorem that: At the point of contact radius is perpendicular to the tangent.

Complete step by step answer:
Let us draw the diagram according to the situation given in the question.

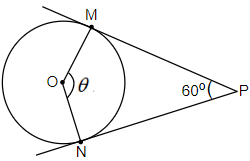
In the above figure, we have considered a circle with centre O. Tangents are drawn from point P, which are PM and PN. We can see that the points of contact of tangent PM and PN with the circle are M and N respectively.
Now, we have joined OM and ON. So, clearly OM and ON are the radius of the circle. We have assumed the angle between these radii as $\theta $. We have to find the value of this $\theta $.
Here, we know that, radius of a circle is perpendicular to the tangent at the point of contact. Therefore, OM is perpendicular to PM and ON is perpendicular to PN.
$ \angle OMP=\angle ONP={{90}^{\circ }}\ldots \ldots \ldots \left( i \right)$
Clearly, we can see that OMNP is a quadrilateral and we know that, sum of all interior angles is equal to ${{360}^{\circ }}$.
$\angle OMP+\angle ONP+{{60}^{\circ }}+\theta ={{360}^{\circ }}$
Substituting the values of $\angle OMP$ and $\angle ONP$ from equation (i), we get,
$\begin{align}
& {{90}^{\circ }}+{{90}^{\circ }}+{{60}^{\circ }}+\theta ={{360}^{\circ }} \\
 & \Rightarrow {{240}^{\circ }}+\theta ={{360}^{\circ }} \\
 & \Rightarrow \theta ={{360}^{\circ }}-{{240}^{\circ }} \\
 & \therefore \theta ={{120}^{\circ }} \\
\end{align}$
Hence, option C is the correct answer.

Note:
One may note that we must draw a rough diagram before solving the question as it will help us to visualize the situation more effectively. Here, we have applied the property of sum of all interior angles of quadrilateral because we knew the values of three angles and there was only one unknown one.