Question

To divide the line segment AB in the ratio \[5:6\] draw a ray AX, such that \[\angle BAX\] is an acute angle. Then draw a ray BY parallel to AX and the points \[{{A}_{1}},{{A}_{2}},{{A}_{3}}...\] and \[{{B}_{1}},{{B}_{2}}{{B}_{3}},...\] are located at equal distances on the ray AX and BY respectively. Then the points joined are ___
(a) \[{{A}_{5}}\] and \[{{B}_{6}}\]
(b) \[{{A}_{6}}\] and \[{{B}_{5}}\]
(c) \[{{A}_{4}}\] and \[{{B}_{5}}\]
(d) \[{{A}_{5}}\] and \[{{B}_{4}}\]

Answer 1

Hint: We solve this problem by using the division of a line segment in the given ratio.
We follow the following steps to divide the line segment in the ratio \[m:n\]
(1) Construct a line segment AB of any length.
(2) Construct a ray AX such that \[\angle BAX\] is an acute angle
(3) Divide the ray AX in the equal length less than 1cm in \[m\] parts and name them as\[{{A}_{1}},{{A}_{2}},{{A}_{3}}...\] because the ratio from the point A is given as \[m\]
(4) Construct a ray BY such that \[\angle ABY\] is an acute angle and \[BY\parallel AX\]
(5) Divide the ray BY in the same length as AX into \[n\] parts and name them as \[{{B}_{1}},{{B}_{2}}{{B}_{3}},...\] because the ratio to the point from the dividing part to B is \[n\]
(6) Then join the points \[{{A}_{m}}\] and \[{{B}_{n}}\] to divide the line segment AB in the ratio \[m:n\]
We follow the above steps to find out which points need to be joined in the given question.

Complete step-by-step solution
We are given that the line segment AB is to be divided in the ratio \[5:6\]
Now, let us draw the line segment AB as follows

Now, let us construct a ray AX such that \[\angle BAX\] is an acute angle then we get

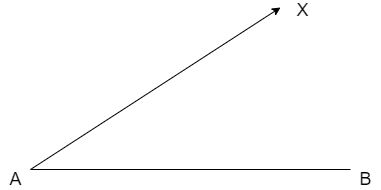
Now, let us divide the ray AX into 5 parts because we are given that the ratio as \[5:6\] then we get

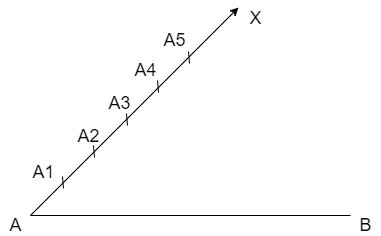
Now let us construct a ray BY such that \[\angle ABY\] is an acute angle and \[BY\parallel AX\] then we get

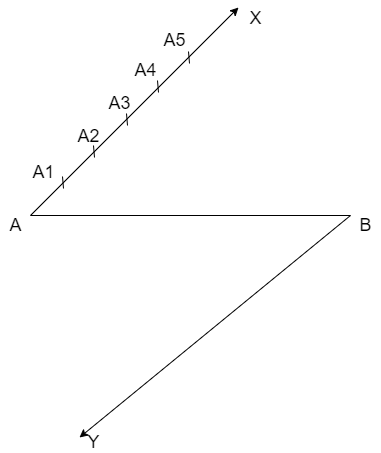
Now let us divide the ray BY into 6 parts of equal length as we did for the ray AX because we are given that the ratio as \[5:6\] then we get

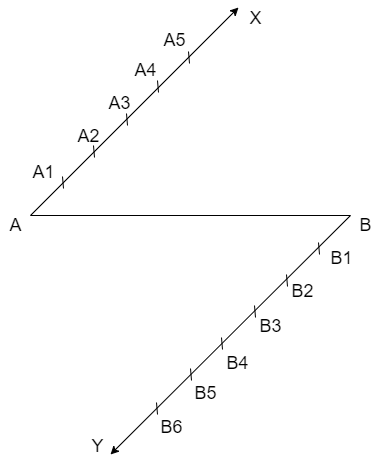
We know that we need to join the points \[{{A}_{m}}\] and \[{{B}_{n}}\] to divide the line segment AB in the ratio \[m:n\]
By using the above condition let us join the points \[{{A}_{5}}\] and \[{{B}_{6}}\] then we get

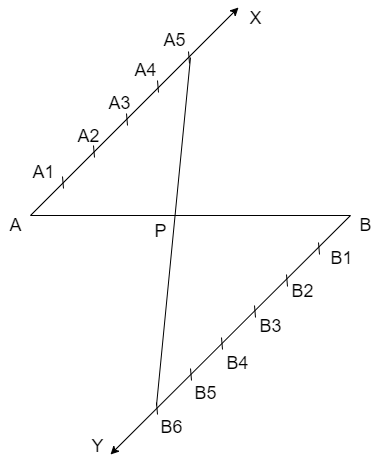
Here, we can see that the point P divides AB in the ratio \[5:6\]
Therefore we can conclude that the points that need to be joined are \[{{A}_{5}}\] and \[{{B}_{6}}\]
So, option (a) is the correct answer.

Note: Students may make mistakes in taking the second ray that is BY.
We need to draw the ray BY such that \[BY\parallel AX\] also we need to keep in mind that the angle \[\angle ABY\] is an acute angle then we get the figure as

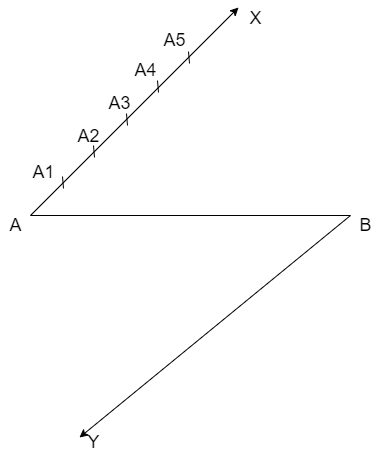
But students may miss the point of taking the angle \[\angle ABY\] is acute and take the figure as

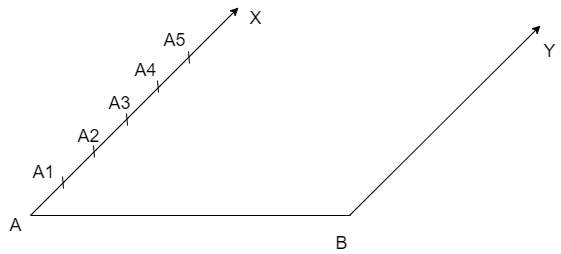
This is wrong because it is used for external division of points but we need the internal division, so we need to use the condition that \[\angle ABY\] is acute and construct the figure accordingly.