Question

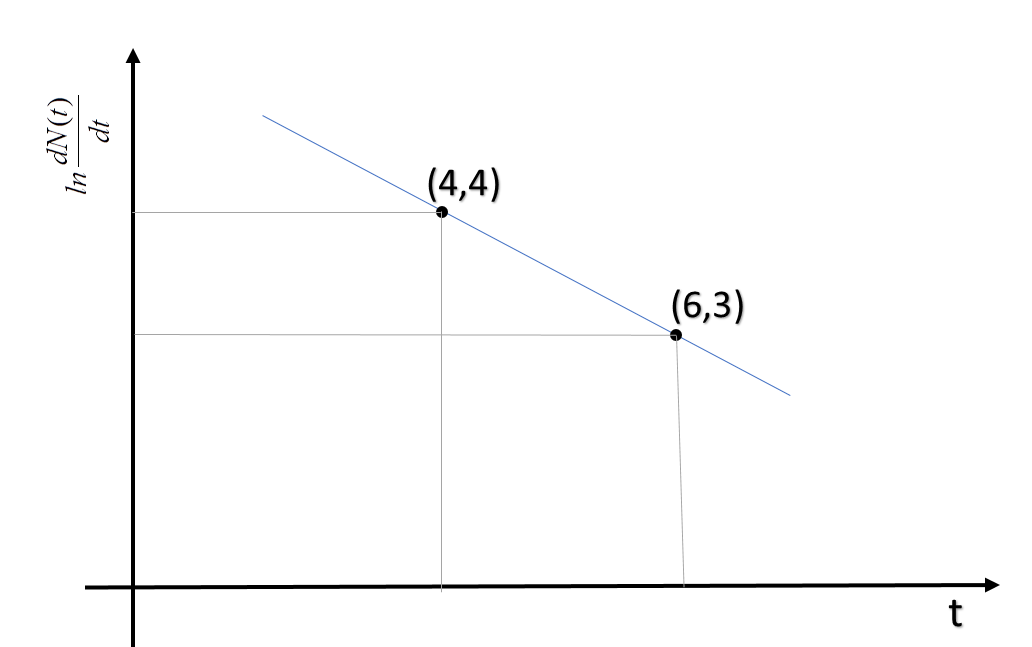
To determine the half-life of a radioactive element, a student plots a graph of $ln \dfrac{dN(t)}{dt}$vs $t$. Here $\dfrac {dN(t)}{dt}$ is the rate of radioactive decay at time ‘t’. If the number of radioactive nuclei of this element decreases by a factor of ‘p’ after 4.16 years, the value of ‘p’ is:

A. 9
B. 8
c. 10
D. 11

Answer 1

Hint: Every radio-active reaction follows first order kinetics, which means that the rate of decay of the element depends is proportional to the first power of the concentration of that element. This states that the element will decay exponentially with the time. We have well derived relations for the concentration of elements undergoing first order reactions.

Formula used:
$N = N_o e^{-\lambda t}$

Complete answer:
As the concentration of an element undergoing first order reaction varies as $N = N_o e^{-\lambda t}$ (here, N is the amount decayed after time ‘t’ from a sample of $N_o$ and $\lambda$ is a constant, called decay constant), we can easily find the rate of change of consternation as;
$N = N_o e^{-\lambda t}$
And $\dfrac{dN}{dt} = -\lambda N_o e^{-\lambda t}$
Now, taking log both sides, we get;
$ln \left[ \dfrac{dN}{dt} \right] = ln \lambda N_o - \lambda t$
Now, from the graph, we can see, the slope of the line which is equal to $\lambda$ is $\dfrac{1}{2}$/year.
Hence, $N = N_o e^{-\lambda t}$
$N_{finally} = \dfrac{N_o}{p} = N_o e^{-\lambda t}$
$\implies p = e^{\lambda t}$
Given time = 4.16 years
So $p = e^{4.16\times \dfrac12} = e^{2.08} \approx 8$
Thus, p is roughly 8.

So, the correct answer is “Option B”.

Additional Information:
Every reaction, whether nuclear or chemical obeys a certain order of reaction. Reaction can be of zeroth order, first order, second order or higher order. The order is decided as per the behavior of each reactant. If the rate of change of concentration of reactant depends upon the power 2 of the concentration, it’s called second order. In that way, the zeroth order reaction doesn’t really depend upon the concentration of the reactant.

Note:
When-ever we have a nuclear reaction, we have to assume it first order unless stated. This is the most important reaction in chemical kinetic theory. These reactions are very useful in the laboratory in which nuclear experiments are conducted (Nuclear fission reaction experiments).