Question

Through the midpoint M of the side CD of a parallelogram ABCD, the line BM is drawn intersecting AC at L and AD produced at E. Prove that $ EL = 2BL $ .

Answer 1

Hint: To derive required proof, we first prove triangles BMC and triangle DME are congruent and then prove triangle ALE and triangle BLC similar and substituting values in ratio of sides obtained from similar triangles to get required proof.

Complete step-by-step answer:
ABCD is a parallelogram. M is the midpoint of CD.

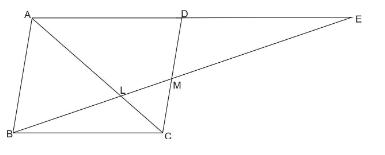
In $ \Delta BCM\,\,and\,\Delta EDM $
CM = DM (M is midpoint of CD)
 $
  \angle BMC = \angle DME\,\,\left( {Vertical\,\,opposite} \right) \\
  \angle BCM = \angle EDM\,\,\left( {alternate\,\,\operatorname{int} erior\,\,angles} \right) \\
  \therefore \Delta BCM \cong \Delta EDM\,\,\left( {ASA\,\,\,congurence} \right) \\
  $
 $ \Rightarrow BC = DE\,\,\,\,\,\,\left( {by\,\,CPCT} \right) $
Also, BC = AD (opposite side of a ||gm ABCD)
Adding above two equations we have,
 $
  BC + BC = AD + DE \\
   \Rightarrow 2BC = AE..............(i) \\
  $
Now, in $ \Delta $ BLC and $ \Delta $ ALE, we have
\[
  \angle EAL = \angle BCL (\because \text{alternate angles}) \\
  \angle BCL = \angle AEL (\because \text{alternate angles})\;
 \]
 $ \therefore \Delta BCL \sim \Delta ELA $
 $
  \Rightarrow \dfrac{{BL}}{{EL}} = \dfrac{{BC}}{{AE}} \\
   \Rightarrow \dfrac{{BL}}{{EL}} = \dfrac{{BC}}{{2BC}} \\
   \Rightarrow \dfrac{{BL}}{{EL}} = \dfrac{1}{2} \\
   \Rightarrow EL = 2BL \;
  $
Which is the required proof.

Note: In geometric proof, to derive required proof we must go through the statement carefully and then use different conditions given in the problem as in either similarities or congruence of triangle to prove required proof asked in question.