
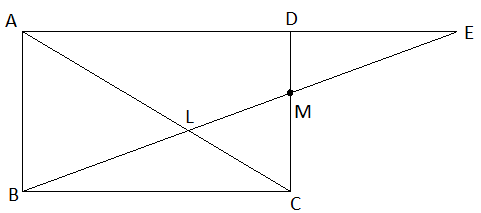
Through the mid-point M of the side CD of a parallelogram ABCD, the line BM is drawn intersecting AC at L and AD produced at E (as shown in the figure below). Prove \[EL=2BL\].

Answer
613.2k+ views
Hint: In the above question, we will consider the \[\Delta BMC\] and \[\Delta EMD\] and make them congruent by ASA criterion of congruence. Also, we will have to use the concept of similarity of triangles between \[\Delta BLC\] and \[\Delta ELA\].
Complete step-by-step answer:
We have been given the figure in the question as below:
In \[\Delta BMC\]and \[\Delta EMD\], we have,
\[\angle BMC=\angle EMD\]
\[\because \]Both angles are vertically opposite angles to each other.
Also, it is given that MC = DM.
\[\angle BCM=\angle EDM\]
\[\because \]Both the angles are alternate interior angle as \[AE||BC\] and DC is the
transversal line.
\[\Delta BMC\cong \Delta EMD\] by ASA congruence criterion of triangles.
Hence, BC = DE according to the corresponding parts of the congruent triangle.
AE = AD + DE = BC + BC = 2 BC….(1)
Now in \[\Delta BLC\] and \[\Delta ELA\], we have,
\[\angle BLC=\angle ALM\]
\[\because \]Both the angles are vertically opposite angles.
\[\angle EAL=\angle BCL\]
\[\because \]Both the angles are alternate interior angles.
\[\Delta BLC\sim \Delta ELA\] by AA similarly.
\[\dfrac{BL}{EL}=\dfrac{BC}{AE}\] by using corresponding parts of a similar triangle.
Now, by using equation (1), we get,
\[\begin{align}
& \dfrac{BL}{EL}=\dfrac{BC}{2BC} \\
& \dfrac{BL}{EL}=\dfrac{1}{2} \\
& EL=2BL \\
\end{align}\]
Hence it is proved that \[EL=2BL\].
Note: Just remember the concept of similarity and congruence of triangles as it will help you a lot in these types of questions.
Also, remember the properties of two parallel lines when cut by a transversal line.
Also, once go through the different criterion of congruence and similarity of a triangle.
Complete step-by-step answer:
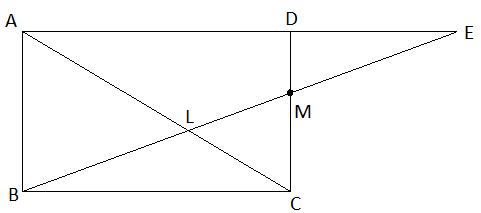
We have been given the figure in the question as below:

In \[\Delta BMC\]and \[\Delta EMD\], we have,
\[\angle BMC=\angle EMD\]
\[\because \]Both angles are vertically opposite angles to each other.
Also, it is given that MC = DM.
\[\angle BCM=\angle EDM\]
\[\because \]Both the angles are alternate interior angle as \[AE||BC\] and DC is the
transversal line.
\[\Delta BMC\cong \Delta EMD\] by ASA congruence criterion of triangles.
Hence, BC = DE according to the corresponding parts of the congruent triangle.
AE = AD + DE = BC + BC = 2 BC….(1)
Now in \[\Delta BLC\] and \[\Delta ELA\], we have,
\[\angle BLC=\angle ALM\]
\[\because \]Both the angles are vertically opposite angles.
\[\angle EAL=\angle BCL\]
\[\because \]Both the angles are alternate interior angles.
\[\Delta BLC\sim \Delta ELA\] by AA similarly.
\[\dfrac{BL}{EL}=\dfrac{BC}{AE}\] by using corresponding parts of a similar triangle.
Now, by using equation (1), we get,
\[\begin{align}
& \dfrac{BL}{EL}=\dfrac{BC}{2BC} \\
& \dfrac{BL}{EL}=\dfrac{1}{2} \\
& EL=2BL \\
\end{align}\]
Hence it is proved that \[EL=2BL\].
Note: Just remember the concept of similarity and congruence of triangles as it will help you a lot in these types of questions.
Also, remember the properties of two parallel lines when cut by a transversal line.
Also, once go through the different criterion of congruence and similarity of a triangle.
Recently Updated Pages
Master Class 10 Computer Science: Engaging Questions & Answers for Success

Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Master Class 10 English: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Master Class 10 Science: Engaging Questions & Answers for Success

Trending doubts
What is the median of the first 10 natural numbers class 10 maths CBSE

Which women's tennis player has 24 Grand Slam singles titles?

Who is the Brand Ambassador of Incredible India?

Why is there a time difference of about 5 hours between class 10 social science CBSE

Write a letter to the principal requesting him to grant class 10 english CBSE

A moving boat is observed from the top of a 150 m high class 10 maths CBSE




