Question

Three weights A, B and C are connected by string as shown in the figure. The system moves over a frictionless pulley. The tension in the string connecting A and B is

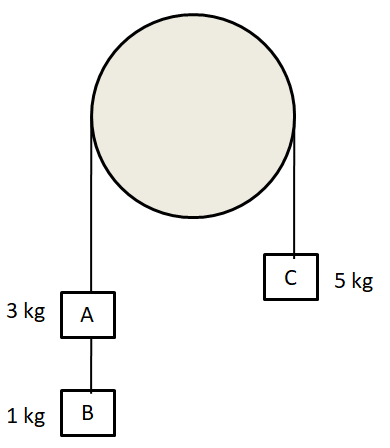
(A) $ g $
(B) $ \dfrac{g}{9} $
(C) $ \dfrac{{8g}}{9} $
(D) $ \dfrac{{10g}}{9} $

Answer 1

Hint
To solve this question, we have to determine the common acceleration of the system. Then, using Newton's second law of motion for the blocks, we can find out the value of the required tension.
Formula Used: The formula used to solve this question is
 $ F = ma $
Here $ F $ is the force acting on a system of mass $ m $ and having an acceleration of $ a $

Complete step by step answer
As can be seen in the figure, there are two strings. Let the tensions in the two strings be $ {T_1} $ and $ {T_2} $ as shown in the diagram below.

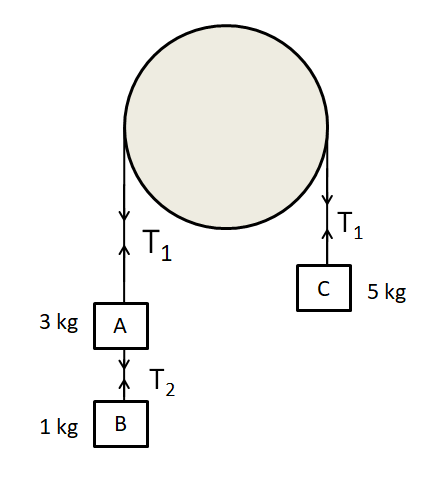
Firstly, we find the common acceleration of the system of the blocks. For this, we consider only the external forces on the system, which are the gravitational forces on each block.

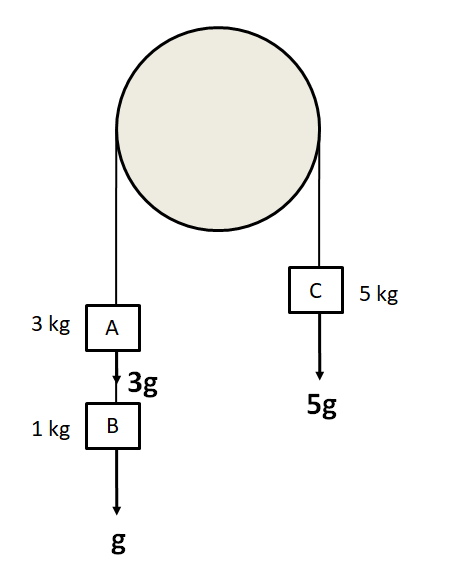
We can see from the figure that the net downward pulling force is
 $ F = 5g - \left( {3g + g} \right) $
 $ F = g $
Total mass of the system $ m = \left( {1 + 3 + 5} \right)kg = 9kg $
Now, we know from the Newton’s second law of motion
 $ F = ma $
 $ a = \dfrac{F}{m} $
Substituting the values, we get
 $ a = \dfrac{g}{9}m/{s^2} $
Therefore, the acceleration of the C block is $ \dfrac{g}{9}m/{s^2} $ downwards, and that of blocks A and B is $ \dfrac{g}{9}m/{s^2} $ upwards.
For determining the tension in the string connecting A and B, that is $ {T_2} $ , we consider the free body diagram of the block B, as shown

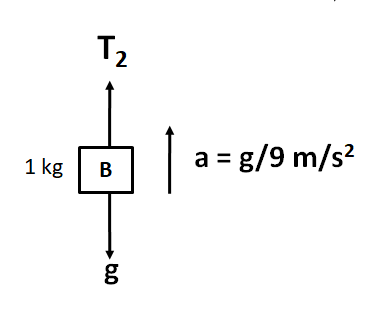
Applying Newton’s second law, we have
 $ {T_2} - g = 1\left( {\dfrac{g}{9}} \right) $
Finally adding $ g $ both the sides, we get
  $ {T_2} = g + \dfrac{g}{9} $
 $ {T_2} = \dfrac{{10g}}{9}N $
Thus, the tension in the string connecting the blocks A and B is $ \dfrac{{10g}}{9} $
Hence, the correct answer is option (D).

Note
For determining the required tension, we could also have determined the tensions $ {T_1} $ and $ {T_2} $ from the equation of motion of the block A and block C. But we should prefer that block to write the equation of motion for, which has minimum number of unknown forces acting on it, so that our time gets saved.
So we chose the block B which has the only unknown force as the force of tension $ {T_2} $ , in which we are interested.