Question

Three vertices of a parallelogram are (a+b, a-b), (2a+b, 2a-b) and (a-b, a+b) taken in order, the fourth vertex is (-b, b). If true enter 1 else 0.

Answer 1

Hint: In this question use the concept that opposite sides of a parallelogram are equal, this means AB=DC and AD=BC of the parallelogram. Take any two of opposite sides and apply distance formula by considering the fourth coordinate (-b,b) . If these distances come out to be the same then surely the fourth quadrant is (-b,b).

Complete step-by-step answer:

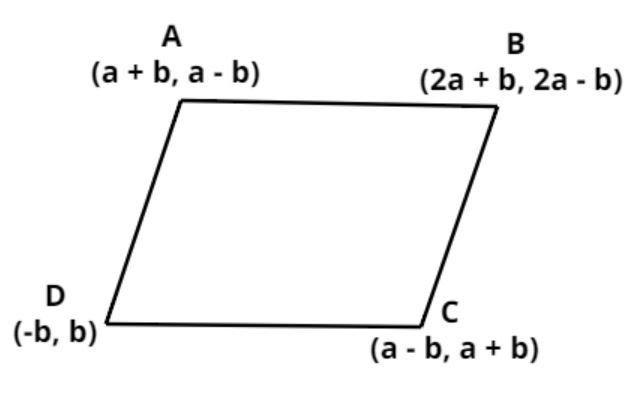
Let us consider the Parallelogram ABCD as shown in figure the coordinates of the three vertices taken in order are also shown we have to check whether the coordinates of the fourth vertex is (-b, b) or not.
As we know that in parallelograms opposite sides are equal.
$ \Rightarrow AB = DC$
I.e. the length of AB should be equal to the length of DC.
As we know the distance (d) formula between two points $(x_1, y_1)$ and $(x_2, y_2)$ is given as
$d = \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}} $
So let A = $(x_1, y_1)$ = (a + b, a – b)
B = $(x_2, y_2)$ = (2a + b, 2a – b)
C = $(x_3, y_3)$ = (a – b, a + b)
D = $(x_4, y_4)$ = (-b, b)
So distance AB = $\sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}} $
$ \Rightarrow AB = \sqrt {{{\left( {2a + b - a - b} \right)}^2} + {{\left( {2a - b - a + b} \right)}^2}} = \sqrt {{a^2} + {a^2}} = a\sqrt 2 $
Now the distance DC = $ \Rightarrow DC = \sqrt {{{\left( {{x_3} - {x_4}} \right)}^2} + {{\left( {{y_3} - {y_4}} \right)}^2}} = \sqrt {{{\left( {a - b + b} \right)}^2} + {{\left( {a + b - b} \right)}^2}} = \sqrt {{a^2} + {a^2}} = a\sqrt 2 $
So as we see that the distance AB = DC
So the coordinates of the fourth vertex is (-b, b).
So the given statement is true.
Hence enter 1.
So this is the required answer.

Note: In this question it is given that sides are taken in order it means that the sides are taken either in clockwise or anti-clockwise direction. Important properties of parallelogram other than the above mentioned property are that opposite sides of a parallelogram are also parallel to each other. It is advised to remember the distance formula as it helps in most geometry questions.