Question

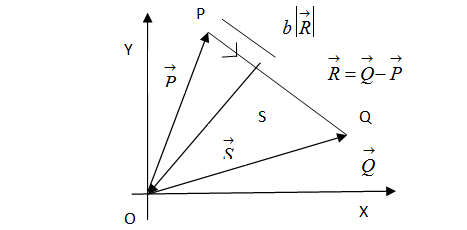
Three vectors $\mathop P\limits^ \to ,\mathop Q\limits^ \to \& \mathop R\limits^ \to $ are shown in the figure. Let S be any point on the vector$\mathop R\limits^ \to $. The distance between the points P and S is b $\left| {\mathop R\limits^ \to } \right|$ .The general relation among vectors $\mathop P\limits^ \to ,\mathop Q\limits^ \to \& \mathop R\limits^ \to $ is:

A) $\mathop S\limits^ \to = \left( {1 - b} \right)\mathop P\limits^ \to + {b^2}\mathop Q\limits^ \to $
B) $\mathop S\limits^ \to = \left( {1 - {b^2}} \right)\mathop P\limits^ \to + b\mathop Q\limits^ \to $
C) $\mathop S\limits^ \to = \left( {1 - b} \right)\mathop P\limits^ \to + b\mathop Q\limits^ \to $
D) $\mathop S\limits^ \to = \left( {b - 1} \right)\mathop P\limits^ \to + b\mathop Q\limits^ \to $

Answer 1

Hint: A vector is a quantity that has both direction and magnitude. The notation of the vector is represented by an arrow over the vector variable.
In the question above we will use the law of vector addition to solve the problem.
In vector addition, the tail of one vector is added with the head of another vector.

Complete step by step solution:
Let’s define the vector first and its properties.
Vectors are geometrical representations of the magnitude and direction of a quantity, where directions are represented by arrows. All the vectors have length which we called magnitude, magnitude of a quantity of our interest. The direction and magnitude of vectors are represented with respect to coordinates such as x, y, z coordinates. The magnitude vector poses are being compared to some other vectors such velocity, displacement, acceleration etc.
Now we will calculate the relationship of vectors asked in the question above:
According to the question:
$\mathop P\limits^ \to + b\mathop R\limits^ \to = \mathop S\limits^ \to $ ( Given to us in the question)......................1
From equation 1 we have
$\mathop R\limits^ \to = \dfrac{{\mathop S\limits^ \to - \mathop P\limits^ \to }}{b}$.................2
We are also provided with:
$\mathop R\limits^ \to = \mathop Q\limits^ \to - \mathop P\limits^ \to $................3
Equating 2 and 3, we obtain
$
   \Rightarrow \dfrac{{\mathop S\limits^ \to - \mathop P\limits^ \to }}{b} = \mathop Q\limits^ \to - \mathop P\limits^ \to \\
   \Rightarrow \mathop S\limits^ \to = \left( {\mathop Q\limits^ \to - \mathop P\limits^ \to } \right)b + \mathop P\limits^ \to \\
   \Rightarrow \mathop S\limits^ \to = \left( {1 - b} \right)\mathop P\limits^ \to + b\mathop Q\limits^ \to \\
 $ (Rearranged the terms on RHS)

Thus, option: C is correct.

Note: We use vectors in breaking the components of a quantity where the actual quantity always remains the hypotenuse. Breaking of the components is generally seen in electrostatics for finding the electric field or force, in finding rolling friction during the motion of the object.