Question

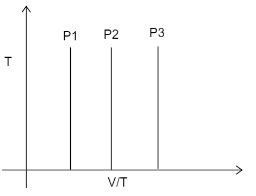
Three times at three different values of constant pressure are given. Which of the following relations is correct?

A) $ {P_1} = {P_2} = {P_3} $
B) $ {P_1} > {P_2} > {P_3} $
C) $ {P_3} > {P_2} > {P_1} $
D) Can be predicted

Answer 1

Hint: To solve this question, we will need to recall the ideal gas equation. The ideal gas equation is given as: $ PV = nRT $
Where, P is the pressure (in atm), V is the volume (in Litres) , n is the total moles of the gas present in the mixture, R is the gas constant and T is the temperature (in Kelvin). The value of R changes with the given Pressure and Volume. The various values of R can be given as: $ 8.314J/K/mol,0.0821Latm/mol,2cal/Kmol $ . This equation is not applicable to Real Gases. If the nature of the gas is not specified, consider it as ideal only.

Complete answer:
In the graph we can see that all the three pressures are given at a constant temperature ‘T’ only. The graph given is T v/s V/T. According to the ideal gas equation: $ PV = nRT $
From this equation we can say that $ P = \dfrac{{nRT}}{V} $ . If we consider n and R to be constant, we get that $ P = \dfrac{T}{V} $ , pressure is inversely proportional to V and directly proportional to T. we are given V/T, in which P is directly proportional to T and inversely proportional to V. The condition given to us is constant temperature (T). Hence as the value of V/T increases P will decrease.
We are given three pressures $ {P_1},{P_2},{P_3} $ . As the value V/T increases the pressure will decrease. The relationship will thus become, $ {P_1} > {P_2} > {P_3} $ .
The correct answer is Option B).

Note:
Alternatively, we can say that, $ V \propto \dfrac{1}{P} $ . Since T is constant, $ V = T.\dfrac{1}{P} $ . This can be written as, $ \dfrac{V}{T} \propto \dfrac{1}{P} $ . Thus, the more the value of V/T lesser will be the value of P. The inverse relationship can also be established like this. The relationship between $ {P_1},{P_2},{P_3} $ will be the same.