Question

Three tangents are drawn at random to a given circle: show that the odds are 3 to 1 against the circle being inscribed in the triangle formed by them.

Answer 1

Hint: Draw three tangents to the circle and construct their parallel lines which are also tangents to the given circle. Then find the total number of combinations of these lines and the number of triangles that can be formed and conclude the answer.

Complete step-by-step answer:

The largest circle inscribed that fits in a triangle is called the incircle of the triangle. The sides of the triangles are then tangents to this circle.

Let us construct a circle and draw three tangents to it at random as shown in the figure.

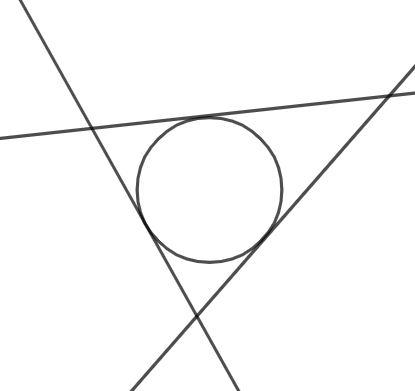
Now construct the parallel lines to each of the tangents such that these three lines are also tangents to the same circle as shown in the figure.

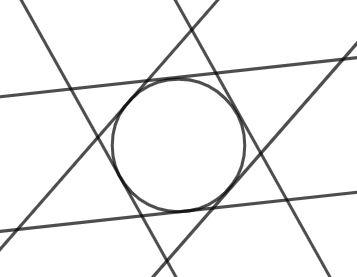
Now, we can observe that it forms a star-like shape. Now, we count the total triangles formed. There are 6 small triangles on the end of the stars and two big triangles inverted to each other that form the star. These two triangles are the ones that contain the circle inside them.

Hence, these are the required triangles. The odds of getting this triangle is given as follows:

\[\dfrac{6}{2} = \dfrac{3}{1}\]

Hence, the odds are 3 to 1 against the circle being inscribed in the triangle formed by the three tangents.

Note: You can also prove this by just considering the three tangents and drawing them in different orientations until you get all the orientations and then you can calculate the odds of getting a triangle such that the circle is contained in them.