Question

Three solid cubes have a face diagonal of $ 4\sqrt 2 {\text{ cm}} $ each. Three other solid cubes have a face diagonal of $ 8\sqrt 2 {\text{ cm}} $ each. All the cubes are melted together to form a big cube. Find the side of the cube formed (in cm).
(A) $ 10 $
(B) $ 12 $
(C) $ 13 $
(D) $ 15 $

Answer 1

Hint: In this question, six solid cubes are melted together in order to form a big cube. So, the volume of the big cube is the total sum of the volume of the six cubes. We know that for a cube, the face of a cube is always a square. For a square having side length, $ a $ the length of the diagonal of a square is given by the formula,
\[{\text{length of diagonal}} = \sqrt 2 \times {\text{side length}}\]

Complete step-by-step answer:
Given:
Three solid cubes having an equal length of the face diagonal given by,
 $\Rightarrow {d_1} = 4\sqrt 2 {\text{ cm}} $
Let us assume the length of the side of the square of these three solid cubes be $ {a_1} $ .
We know that the face of a cube is a square and the diagonal of the square is $ \sqrt 2 $ times the length of the side of the square.
So, we get, for first three cubes,
 $\Rightarrow {d_1} = \sqrt 2 \times {a_1} $
Substituting $ {d_1} = 4\sqrt 2 {\text{ cm}} $ we get,
 $\Rightarrow 4\sqrt 2 = \sqrt 2 \times {a_1} $
Solving this, we get,
 $\Rightarrow {a_1} = 4{\text{ cm}} $
So, the volume of the three cubes = $ 3 \times $ volume of one cube
 $\Rightarrow {V_1} = 3 \times {a_1}^3 $
Substituting $ {a_1} = 4{\text{ cm}} $ we get,
 $
\Rightarrow{V_1} = 3 \times {4^3}\\
 = 3 \times 64\\
 = 192{\text{ c}}{{\text{m}}^3}
 $
Similarly,
For three other solid cubes having the same length of the face diagonal given by-
 $\Rightarrow {d_2} = 8\sqrt 2 {\text{ cm}} $
Also, let us assume the length of the side of the square of these other three solid cubes be $ {a_2} $ .
Then for the three other cubes, the length of the diagonal of the square $ {d_2} = \sqrt 2 \times {a_2} $
Substituting $ {d_2} = 8\sqrt 2 {\text{ cm}} $ we get,
 $\Rightarrow 8\sqrt 2 = \sqrt 2 \times {a_2} $
Solving this we get,
 $\Rightarrow {a_2} = 8{\text{ cm}} $
So, the volume of the other three cubes = $ 3 \times $ volume of one cube
 $\Rightarrow {V_2} = 3 \times {a_2}^3 $
Substituting $ {a_1} = 8{\text{ cm}} $ we get,
 $
\Rightarrow{V_2} = 3 \times {8^3}\\
 = 3 \times 512\\
 = 1536{\text{ c}}{{\text{m}}^3}
 $

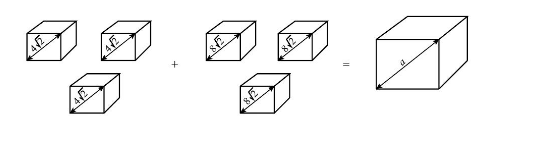
Now, the total volume of all the six cubes combined $ V = {V_1} + {V_2} $
Substituting the values of $ {V_1} $ and $ {V_2} $ we get,
 $
\Rightarrow V = 192 + 1536\\
 = 1728{\text{ c}}{{\text{m}}^3}
 $
Let the side of this big cube be $ a $ then, its volume is,
 $
\Rightarrow V = {a^3}\\
1728 = {a^3}
 $
Taking cube roots of both sides we get,
 $\Rightarrow a = 12{\text{ cm}} $
Therefore, the side of the big cube formed after melting all cubes is $ 12{\text{ cm}} $ and the correct option is-
(B) $ 12 $

So, the correct answer is “Option B”.

Note: A cube has a total of six faces and each face is a square and to calculate the length of the diagonal of the square, we use the Pythagoras theorem. So, for a square having side length, $ a $ the length of the diagonal $ d $ is given by,
 $
d = \sqrt {{a^2} + {a^2}} \\
 = \sqrt {2{a^2}} \\
 = \sqrt 2 a
 $