Question

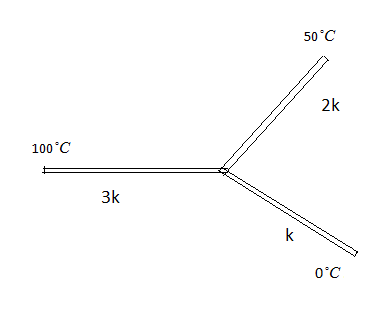
Three rods of the same dimensions have thermal conductivities 3K, 2K and k. They are arranged as shown, with their ends at 100${}^{\circ }C$, 50${}^{\circ }C$ and 0${}^{\circ }C$. The temperature of their junction is:

(A) $75^0$
(B) $\dfrac{200}{3}^0$
(C) $40^0$
(D) $\dfrac{100}{3}^0$

Answer 1

Hint: Thermal conductivity of a material gives us an idea about the heat transfer in a material body. In the above problem, we have to understand the fact that the total heat incoming will be equal to the total heat outgoing. Moreover, heat always flows from a hotter region to a colder region, so at the junction, the rod will be at an equilibrium temperature.

Formula used:
The quantity of heat flow in a body is given by:
$Q=\dfrac{KA(\Delta T)}{L}$

Complete step-by-step answer:
Given,
The 3 rods are of the same dimension and at different temperatures with different values of thermal conductivities.
${{K}_{1}}=3K$
$\begin{align}
  & {{K}_{2}}=2K \\
 & {{K}_{3}}=K \\
\end{align}$
$\begin{align}
  & {{T}_{1}}=100{}^{\circ }C \\
 & {{T}_{2}}={{50}^{\circ }}C \\
 & {{T}_{3}}={{0}^{\circ }}C \\
\end{align}$
Let the temperature at the junction be given by T.
For heat flow we have,
$Q=\dfrac{KA(\Delta T)}{L}$
Where Q is the quantity of heat
K is the thermal conductivity
A is the area
$\Delta T$ is the change in temperature
L is the length of the rod
Since the dimensions are the same, the length and area of the rod will be the same in the three cases.
Therefore, we have
Incoming heat=Outgoing heat
$\Rightarrow {{Q}_{1}}={{Q}_{2}}+Q{}_{3}$
$\begin{align}
  & \Rightarrow \dfrac{{{K}_{1}}\times A\times ({{T}_{1}}-T)}{L}=\dfrac{{{K}_{2}}\times A\times ({{T}_{2}}-T)}{L}+\dfrac{{{K}_{3}}\times A\times ({{T}_{3}}-T)}{L} \\
 & \Rightarrow 3K\times (100-T)=2K\times (50-T)+K\times (0-T) \\
 & \Rightarrow 300-3T=2T-100+T \\
 & \Rightarrow 400=6T \\
 & \Rightarrow T={{\dfrac{200}{3}}^{\circ }}C \\
\end{align}$
Thus, the correct option is $T={{\dfrac{200}{3}}^{\circ }}C$. So, the temperature at the junction of the 3 rods is (B)${{\dfrac{200}{3}}^{\circ }}C$

So, the correct answer is “Option B”.

Additional Information: The thermal conductivity of a material is a measure of its heat transfer. The bodies with lower thermal conductivity give off heat at a lower rate than the bodies with higher thermal conductivity. Thermal conduction is generally defined as the transport of energy due to random molecular motion across a temperature gradient.

Note: In this problem, the most important thing to be kept in mind is that the incoming heat is equal to the outgoing heat. The temperature at the junction will be lesser than 100 degree Celsius and more than 50 degree Celsius since heat flows from a hotter region to a colder region until it reaches equilibrium. So the temperature at the junction is the equilibrium temperature.