Question

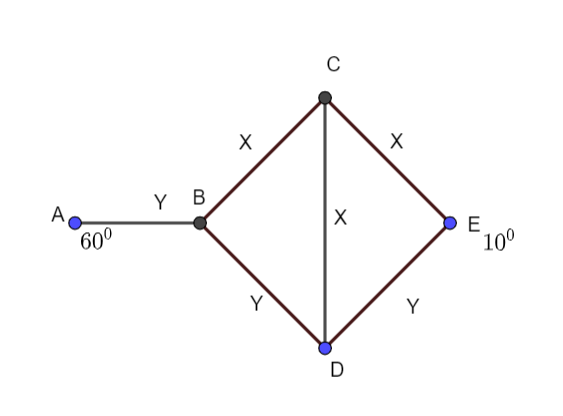
Three rods of material X and three rods of material Y are connected as shown in the figure. All the rods are identical in length and cross-sectional area. If the end A is maintained at ${60^0}$ and the junction E at ${10^0}$ , calculate the temperatures of the junctions B, C and D. The thermal conductivity of X is $0.92$ CGS units and that of Y is $0.46$ CGS units.

Answer 1

Hint: In this question, we will first derive a relationship between the thermal resistance of rod X and rod Y using the values of thermal conductivities given in the question. The difference in temperature is given by $\Delta \theta = IR$ where I is the current flowing in the system and R is the thermal resistance. For every arm we will calculate the net resistance and the current flowing through it and substitute the values in the physical relation and find the temperature of the junctions.

Complete step by step solution:
The thermal resistance of a rigid body is inversely proportional to the thermal conductivity of the material.
The mathematical expression is $R \propto \dfrac{1}{K}$ where R is the thermal resistance and K is the thermal conductivity.
For the rods X and Y we have,
${R_X} \propto \dfrac{1}{{{K_X}}}\,,\,{R_Y} \propto \dfrac{1}{{{K_Y}}}$
Further simplifying this we have,
$\dfrac{{{R_X}}}{{{R_Y}}} = \dfrac{{{K_Y}}}{{{K_X}}}$
The thermal conductivity of X is $0.92$ CGS units and that of Y is $0.46$ CGS units.
$\dfrac{{{K_Y}}}{{{K_X}}} = \dfrac{{0.46}}{{0.92}}$
Further solving this we get,
$\dfrac{{{K_Y}}}{{{K_X}}} = \dfrac{1}{2}$
Hence, we can say that $\dfrac{{{R_X}}}{{{R_Y}}} = \dfrac{{{K_Y}}}{{{K_X}}} = \dfrac{1}{2}$
Let the resistance ${R_X}$ be $R$ . The resistance ${R_Y}$ will be $2R$
Now the difference in temperature is given by $\Delta \theta = IR$ where I is the current flowing in the system and R is the thermal resistance.
Between A and B,
Suppose a current I is flowing.
The thermal resistance is equal to $2R$ .
So, the difference in temperature is given by ${\theta _A} - {\theta _B} = 2RI$
It is given that ${\theta _A} = {60^0}$
Hence, ${60^0} - {\theta _B} = 2RI$
Between B and C,
The current gets divided at junction B. The current flowing in the arm BC is given by ${I_{BC}} = I \times \dfrac{{4R}}{{6R}}$
The thermal resistance is equal to $R$ .
So, the difference in temperature is given by ${\theta _B} - {\theta _C} = \dfrac{{2I}}{3}$
Between B and D,
The current gets divided at junction B. The current flowing in the arm BD is given by ${I_{BD}} = I \times \dfrac{{2R}}{{6R}}$
The thermal resistance is equal to $2R$ .
So, the difference in temperature is given by ${\theta _B} - {\theta _D} = \dfrac{{2I}}{3}$
It can be noticed that ${\theta _B} - {\theta _D} = {\theta _B} - {\theta _C}$
Hence, we can say that junctions C and D are at the same temperature. So, the rod in the middle of the bridge will not carry any current.
The effective resistance between points A and E will be
${R_{eff}} = R + {R_{bridge}}$
Substituting the values, we get,
${R_{eff}} = 2R + \dfrac{{2R \times 4R}}{{2R + 4R}}$
Further solving this equation, we get,
${R_{eff}} = 2R + \dfrac{{4R}}{3}$
$ \Rightarrow {R_{eff}} = \dfrac{{10R}}{3}$
Between A and E,
The current flowing is equal to I.
The effective resistance is $\dfrac{{10R}}{3}$
The difference in temperature is given by ${\theta _A} - {\theta _E} = \dfrac{{10RI}}{3}$
It is given that ${\theta _A} = {60^0}$ and ${\theta _E} = {10^0}$ .
$ \Rightarrow {\theta _A} - {\theta _E} = {50^0}$
Substituting in the equation we get,
${\theta _A} - {\theta _E} = 50 = \dfrac{{10IR}}{3}$
Further solving this we get,
$IR = 15$
We calculated that ${60^0} - {\theta _B} = 2RI$
Substituting the value, we get,
${60^0} - {\theta _B} = 2 \times 15$
Further solving this we get,
${60^0} - {30^0} = {\theta _B}$
$ \Rightarrow {\theta _B} = {30^0}$
We calculated that ${\theta _B} - {\theta _C} = \dfrac{{2I}}{3}$
Substituting the value, we get,
$30 - {\theta _C} = \dfrac{{2 \times 15}}{3}$
Further solving this we get,
$30 - {\theta _C} = 10$
$ \Rightarrow {\theta _C} = {20^0}$
The temperature of junctions C and D is same and so ${\theta _D} = {20^0}$

Note: The term current can be misleading. Here it means thermal current. Thermal current is the flow of heat. The thermal system is synonymous as a whole with the electric system. The potential gradient is analogous to the temperature difference which acts as the driving force. The resistance is analogous to the thermal resistance while current to the thermal current.