Question

Three rods of identical cross-sectional area and made from the same metal form the sides of an isosceles triangle ABC, right angled at B. The points A and B are maintained at temperatures T and $\left( \sqrt{2}T \right)$ respectively. In the steady state, the temperature of the point C is ${{T}_{c}}$. Assuming that only heat conduction takes place, the value of $\dfrac{T}{{{T}_{c}}}$ is

Answer 1

Hint:Assume that the temperature at point C, i.e. ${{T}_{c}}$, is higher than the temperature at point A but lower than the temperature at point B. Then apply a conduction formula for rate of heat flow and equate the rate through the rods BC and CA.

Formula used:
$\dfrac{dQ}{dt}=\dfrac{kA({{T}_{2}}-{{T}_{1}})}{l}$
where $\dfrac{dQ}{dt}$ is the arte of heat flow through a conductor of length l, cross section area A and conductivity k. ${{T}_{2}}$ and ${{T}_{1}}$ are the temperatures of the end points

Complete step by step answer:
Let us first draw a figure from the understanding of the given data.

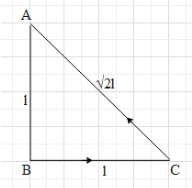
Here, let us assume that the temperature at point C, i.e. ${{T}_{c}}$, is higher than the temperature at point A but lower than the temperature at point B. We know that heat flows from a point at higher temperature to a point that is at a lower temperature. Therefore, the heat flow will be from point C to point A through rod AC and from point B to point C on the rod BC.Therefore, the heat flows from point B to point A via rods BC and CA.

Since it is given that the system is in steady state, the end point temperatures will be constant and the rate of flow of heat will also be constant. In addition, the rate of heat flow through BC is equal to rate flow of heat flow through CA.
${{\left( \dfrac{dQ}{dt} \right)}_{BC}}={{\left( \dfrac{dQ}{dt} \right)}_{CA}}$
$\Rightarrow \dfrac{kA({{T}_{B}}-{{T}_{C}})}{{{l}_{BC}}}=\dfrac{kA({{T}_{C}}-{{T}_{A}})}{{{l}_{CA}}}$ …. (i)

Since both the rods are of the same metal, their conductivity is the same, i.e. k.
Also it is given that the two rods have the same cross sectional area.
Let the length of BC be l. Since it is an isosceles triangle, $BC=AB=l$.
Then, by Pythagoras theorem we get, ${{(CA)}^{2}}={{l}^{2}}+{{l}^{2}}=2{{l}^{2}}$.
$\Rightarrow (AC)=\sqrt{2}l$
Therefore, ${{l}_{BC}}=l$ and ${{l}_{CA}}=\sqrt{2}l$
And it is given that ${{l}_{A}}=T,{{l}_{B}}=\sqrt{2}T$
Substitute the known values in equation (i).
$\Rightarrow \dfrac{kA\left( \sqrt{2}T-{{T}_{C}} \right)}{l}=\dfrac{kA\left( {{T}_{C}}-T \right)}{\sqrt{2}l}$
$\Rightarrow \sqrt{2}\left( \sqrt{2}T-{{T}_{C}} \right)=\left( {{T}_{C}}-T \right)$
$\Rightarrow 2T-\sqrt{2}{{T}_{C}}={{T}_{C}}-T$
$\therefore 3T=\left( \sqrt{2}+1 \right){{T}_{C}}$

This gives us that $\dfrac{T}{{{T}_{C}}}=\dfrac{\left( \sqrt{2}+1 \right)}{3}$.

Note:We could apply this formula of conduction only because it is given that the flow is steady and the heat is flow due to conduction only.It is necessary that we have to assume that the temperature of point C is in between the temperatures of the other two points. Otherwise, the rate of heat flow would not be constant.