Question

Three rods each of mass $M$ and length $L$, are joined together to form an equilateral triangle. What is the moment of inertia of a system about an Axis passing through its centre of mass and perpendicular to the plane of the triangle?

Answer 1

Hint: The centre of mass of a distribution of mass in space is the unique point where the weighted relative position of the distributed mass sums to zero. It can also be said that when a force is applied on this point, then linear motion takes place and no angular motion takes place.

Complete step by step answer:
In this question, the parallel axis theorem will be applied which states that that the moment of inertia of a body about any axis is equal to the moment of inertia about parallel axis through its centre of mass plus the product of the mass of the body and the square of the perpendicular distance between the two parallel axes.
The formula for parallel axis theorem is:
$I = {I_C} + M{h^2}$
Where,
\[I = \] moment of inertia of the body
${I_C} = $ moment of inertia about the centre
$M = $ mass of the body
$h = $ distance between the two axis

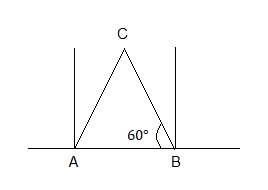
We know that the moment of inertia of a single rod about an axis passing through its centre and perpendicular to it is $\dfrac{1}{{12}}M{L^2}$.
As the rods form an equilateral triangle, the centre of mass of the system will be at the centroid of the triangle.
Now, let $d$ be the distance between the centroid and any one of the sides
$\dfrac{d}{{\dfrac{L}{2}}} = \tan {30^ \circ }$
$d = \dfrac{L}{2} \times \tan {30^ \circ }$
On putting the value of $\tan {30^ \circ }$, we get,
$d = \dfrac{L}{{2\sqrt 3 }}.......(1)$
By parallel axis theorem we can say that moment of inertia of each side of the equilateral triangle about an axis passing through the triangle's centre and perpendicular to its plane is
$I = {I_C} + M{h^2}$
$I = \dfrac{1}{{12}}M{L^2} + M{\left( {\dfrac{L}{{2\sqrt 3 }}} \right)^2}$
On further solving, we get,
$I = \dfrac{1}{{12}}M{L^2} + \dfrac{1}{{12}}M{L^2}$$I = \dfrac{1}{6}M{L^2}$
$I = \dfrac{1}{6}M{L^2}$
So, the moment of inertia of the triangle about this axis is then
${I_{eq}} = 3 \times \dfrac{1}{6}M{L^2}$ (the sum of moment of inertia of each rod is the moment of inertia of the system)
${I_{eq}} = \dfrac{1}{2}M{L^2}$
So, the final answer is ${I_{eq}} = \dfrac{1}{2}M{L^2}$.

Note: The torque required for acceleration about the rotational axis is determined by moment of inertia. The sum of moment of inertia of each rod gives the moment of inertia of the system. It is also important to note that the moment of inertia is also called rotational inertia. The moment of inertia gives the relationship for the dynamic of rotational motion.