Question

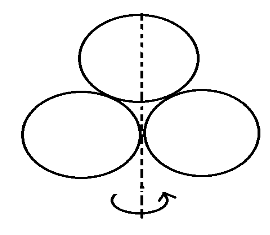
Three rings each of mass $m$ and radius $r$ are so placed that they touch each other. The radius of gyration of the system about the axis as shown in the figure is:

Answer 1

Hint:In the question, we are provided with three identical rings of given mass and radius. We have to find the radius of gyration of the system. For that we need to find the total moment of inertia. Moment of inertia about its diameter is $\dfrac{1}{2}m{r^2}$ and moment of inertia about its axis perpendicular to the plane passing through radius is $m{r^2}$.

Complete step by step answer:
Consider three identical rings as shown in the diagram each having mass $m$ and radius $r$. We have to find the radius of gyration of the system about its axis. For that we need to find the total moment of inertia of the system.Firstly, finding the moment of inertia of the upper ring about its axis ${I_1} = \dfrac{1}{2}m{r^2}$
Moment of inertia of one of the lower rings about its axis ${I_2} = \dfrac{1}{2}m{r^2} + m{r^2} = \dfrac{3}{2}m{r^2}$ (adding Moment of inertia about its axis and along the perpendicular to the plane)
Similarly, moment of inertia of the other ring be ${I_3} = \dfrac{3}{2}m{r^2}$
Total moment of inertia be $I = {I_1} + {I_2} + {I_3}$
$
I = \dfrac{1}{2}m{r^2} + \dfrac{3}{2}m{r^2} + \dfrac{3}{2}mr \\
\Rightarrow I = \dfrac{7}{2}m{r^2} \\ $
Radius of gyration $\left( k \right)$:
$k = \sqrt {\dfrac{I}{M}} $
where $I$ is the total moment of inertia of the system
$M$ is the total mass of the system.
$
M = m + m + m \\
\Rightarrow M = 3m \\ $
$\Rightarrow k = \sqrt {\dfrac{{\dfrac{7}{2}m{r^2}}}{{3m}}} = \sqrt {\dfrac{{7{r^2}}}{6}} $
$\therefore k = r\sqrt {\dfrac{7}{6}} $
This is our required answer.

Note:Ring has greater moment of inertia than the circular disc having the same mass and radius, about its axis passing through its center of mass perpendicular to the plane.Because the entire mass is concentrated at a maximum distance about its axis.