Question

Three points A, B and C are on the straight bank of a river such that $BC=2km$. A boat is moving towards B on a line at right angles to the bank. At some point AC subtends an angle of ${{60}^{\circ }}$. After moving for 10 minutes in the same direction AC subtends an angle of ${{120}^{\circ }}$. The speed of boat is:
(a)$4\sqrt{3}km/hr$
(b)$16\sqrt{3}km/hr$
(c) $8\sqrt{3}km/hr$
(d) $24\sqrt{3}km/hr$

Answer 1

Hint: First of all, draw the figure according to the requirement of the problem. Then we are asked to find the speed of the boat. As in the above options, all the units are given in $km/hr$ so we are assuming the speed of the boat as $xkm/hr$. In solving the problem, we are going to use $\tan \theta $ of a right angled triangle, which is equal to $\dfrac{P}{B}$ where “P” is the perpendicular and “B” is the base of the triangle corresponding to angle $\theta $.

Complete step-by-step answer:
In the below diagram, we have shown three points A, B and C lying on the straight bank of a river with distance between B and C is 2 km. After that, we have shown a boat coming towards B at a right angle to the bank in which AC is subtending an angle of ${{60}^{\circ }}$ onto the point B.

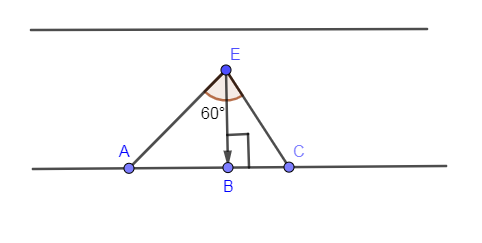
The two parallel lines are showing the two banks of a river. We have shown the boat by point E which is coming at right angles to the bank towards B.
Now, after moving for 10 minutes in the same direction AC subtends an angle of ${{120}^{\circ }}$ on the new position of the boat which we are shown in the below diagram.

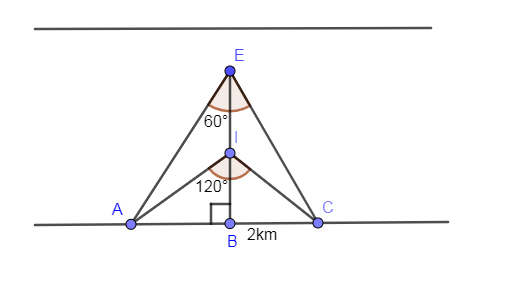
In the above figure, $\Delta EBC$ is a right angled triangle in which $\angle CEB=\dfrac{1}{2}\angle AEC$ so the value of angle CEB is equal to:
$\begin{align}
  & \dfrac{1}{2}\left( {{60}^{\circ }} \right) \\
 & ={{30}^{\circ }} \\
\end{align}$
As $\Delta EBC$ is a right angled triangle so the value of $\angle ECB$ is equal to:
$\begin{align}
  & {{90}^{\circ }}-{{30}^{\circ }} \\
 & ={{60}^{\circ }} \\
\end{align}$
Showing angle ${{60}^{\circ }}$ in $\Delta EBC$ we get,

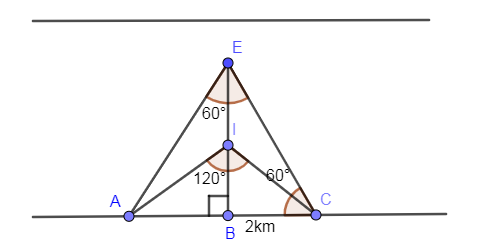
In $\Delta EBC$, we are going to apply $\tan {{60}^{\circ }}$ we know that:
$\tan \theta =\dfrac{P}{B}$
In the above expression, “P” and “B” represents perpendicular and base of the right angled triangle EBC with respect to angle $\theta $ so using the above relation, we are going to find $\tan {{60}^{\circ }}$.
$\tan {{60}^{\circ }}=\dfrac{P}{B}$
Substituting “P” as EB and “B” as BC in the above equation we get,
$\tan {{60}^{\circ }}=\dfrac{EB}{BC}$
We also know that the value of $\tan {{60}^{\circ }}=\sqrt{3}$ so using this relation in the above equation we get,
$\sqrt{3}=\dfrac{EB}{BC}$
Substituting BC as 2 km in the above we get,
$\begin{align}
  & \sqrt{3}=\dfrac{EB}{2} \\
 & \Rightarrow EB=2\sqrt{3}km..........(1) \\
\end{align}$
Similarly, $\Delta IBC$ is also a right angled triangle so $\angle BIC=\dfrac{1}{2}\angle AIC$ and measure of $\angle AIC={{120}^{\circ }}$ so substituting this value of angle AIC in $\angle BIC=\dfrac{1}{2}\angle AIC$ we get,
$\begin{align}
  & \angle BIC=\dfrac{1}{2}\left( {{120}^{\circ }} \right) \\
 & \Rightarrow \angle BIC={{60}^{\circ }} \\
\end{align}$
Now, as $\Delta IBC$ is also a right angled triangle so we the measure of $\angle ICB$ is equal to:
$\begin{align}
  & {{90}^{\circ }}-{{60}^{\circ }} \\
 & ={{30}^{\circ }} \\
\end{align}$
Showing angle ${{30}^{\circ }}$ in $\Delta IBC$ we get,

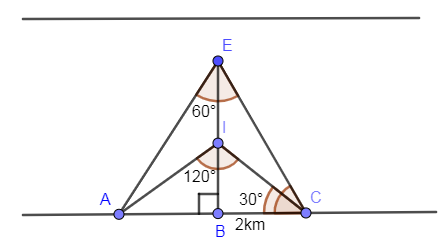
Applying $\tan {{30}^{\circ }}$ in right angle triangle $\Delta IBC$ we get,
$\tan {{30}^{\circ }}=\dfrac{P}{B}$
Substituting “P” as IB and “B” as BC in the above equation we get,
$\begin{align}
  & \tan {{30}^{\circ }}=\dfrac{IB}{BC} \\
 & \Rightarrow \dfrac{1}{\sqrt{3}}=\dfrac{IB}{2} \\
 & \Rightarrow IB=\dfrac{2}{\sqrt{3}} \\
\end{align}$
Rationalizing above expression by multiplying and dividing by $\sqrt{3}$ we get,
$\begin{align}
  & IB=\dfrac{2\sqrt{3}}{\sqrt{3}\times \sqrt{3}} \\
 & \Rightarrow IB=\dfrac{2\sqrt{3}}{3}km.........(2) \\
\end{align}$
Now, the distance EI is equal to:
$EB-IB$
Using (1) and (2) in the above we get,
$\begin{align}
  & \left( 2\sqrt{3}-\dfrac{2\sqrt{3}}{3} \right)km \\
 & =2\sqrt{3}\left( 1-\dfrac{1}{3} \right)km \\
 & =2\sqrt{3}\left( \dfrac{3-1}{3} \right)km \\
 & =2\sqrt{3}\left( \dfrac{2}{3} \right)km \\
 & =\dfrac{4}{\sqrt{3}}km \\
\end{align}$
Hence, the distance EI is equal to $\dfrac{4}{\sqrt{3}}km$
Now, the boat has travelled from E to I in 10 minutes with a speed of x km/hr so using the relation between speed, distance and time.
$\text{Speed}=\dfrac{\text{Distance}}{\text{Time}}$ …………….(3)
Converting 10 minutes into hours we get,
$\begin{align}
  & \dfrac{10}{60}hrs \\
 & =\dfrac{1}{6}hrs \\
\end{align}$
Substituting speed as x km/hr, time as $\dfrac{1}{6}$ hrs and distance as EI in (3) we get,
$\begin{align}
  & x=\dfrac{EI}{\dfrac{1}{6}} \\
 & \Rightarrow x=6EI \\
 & \Rightarrow EI=\dfrac{x}{6} \\
\end{align}$
From the above, we have calculated the value of EI as $\dfrac{4}{\sqrt{3}}km$ so using this relation in the above equation we get,
$\dfrac{4}{\sqrt{3}}=\dfrac{x}{6}$
Multiplying 6 on both the sides we get,
$\dfrac{24}{\sqrt{3}}=x$
Multiplying and dividing by $\sqrt{3}$ we get,
$\begin{align}
  & \dfrac{24\sqrt{3}}{3}=x \\
 & \Rightarrow x=8\sqrt{3}km/hr \\
\end{align}$
Hence, the correct option is (c).

So, the correct answer is “Option (c)”.

Note: In the above solution, make sure you have converted the units first before putting them in the formulas. For instance in the above solution, we have used the relation between speed, distance and time. The distance is in km and speed is in km/hr but we have given the time in 10 minutes so first of all, convert the time into hours by dividing it to 60 then substitute this time in the formula.