Question

Three point masses ${m_1}$​, ${m_2}$ and ${m_3}$ are placed at three corners of a light equilateral triangle of side a. The moment of inertia of the system about an axis coinciding with the altitude of the triangle passing through ${m_1}$​ is:
A. ${m_1} + {m_2} + {m_3}$
B. $\dfrac{{({m_2} + {m_3}){a^2}}}{6}$
C. $\dfrac{{{{({m_2} + {m_3})}^2}}}{{{a^2}}}$
D. $\dfrac{{({m_2} + {m_3}){a^2}}}{4}$

Answer 1

Hint: Inertia is the resistance to change. Whether it can be change of state or change of direction. Usually we call mass as the measurement of inertia because it tells how much resistance is given for linear acceleration when force is applied. Similarly moment of inertia tells us the resistance given for the angular acceleration when torque is applied.

Complete step by step answer:
Since the moment of inertia is the resistance for the angular acceleration there should be a rotating body. When a body is rotating there will be an axis of rotation. The axis about which the body is rotating is called the axis of rotation and we determine the moment of inertia about the axis of rotation. Moment of inertia of a mass about the axis of rotation is the product of mass and its perpendicular distance from the axis of rotation.
Since masses are put at the corners of the equilateral triangle and we are asked to find out the moment of inertia about the altitude, we should know the properties of the equilateral triangle.
In the equilateral triangle the length of three sides will be equal and the angle between any two sides will be 60 degrees. The point of intersection of medians and the point of intersection of altitudes will be the same for an equilateral triangle.
The altitude for any side passes through the corner which is exactly opposite to that side and passes through the midpoint of that side.
The below diagram depicts the question given

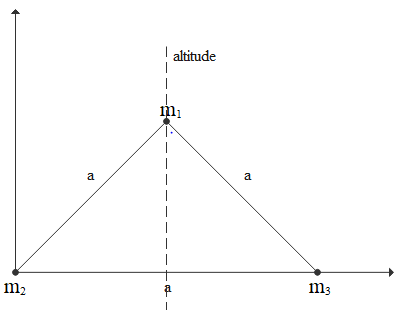
Moment of inertia of mass ${m_1}$ about the altitude will be zero as the altitude passes through the mass itself, perpendicular distance will be zero.
Distance between mass ${m_2}$ and altitude is half of its side length(a) and distance between mass ${m_3}$ will also be the half the side length.
So moment of inertia of ${m_2}$ about the altitude will be
$I = m{r^2}$
$\eqalign{
  & \Rightarrow {I_2} = {m_2}{\left( {\dfrac{a}{2}} \right)^2} \cr
  & \Rightarrow {I_2} = \dfrac{{{m_2}{a^2}}}{4} \cr} $
moment of inertia of ${m_3}$ about the altitude will be
$I = m{r^2}$
$\eqalign{
  & \Rightarrow {I_3} = {m_3}{\left( {\dfrac{a}{2}} \right)^2} \cr
  & \Rightarrow {I_3} = \dfrac{{{m_3}{a^2}}}{4} \cr} $
So moment of inertia of total system about altitude will be
$\eqalign{
  & {I_2} + {I_3} = \left( {\dfrac{{{m_2}{a^2}}}{4} + \dfrac{{{m_3}{a^2}}}{4}} \right) \cr
  & \therefore {I_{total}} = \dfrac{{\left( {{m_2} + {m_3}} \right){a^2}}}{4} \cr} $

Hence option D will be the answer.

Note:
Centroid and the center of mass of a system are completely different. Centroid is the geometrical center of the triangle which is independent of the masses while center of mass is the point where the entire mass is assumed to be concentrated and this depends upon the masses present at the corners of the triangle.