Question

Three masses ${m_1}$,${m_2}$ and ${m_3}$ are attached to a string as shown in the figure. All three masses are held at rest and then released. To keep ${m_3}$ at rest, the condition is:

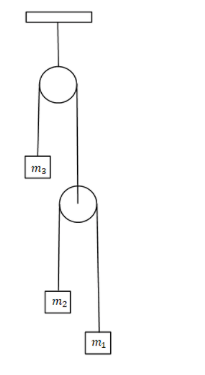
A) $\dfrac{1}{{{m_3}}} = \dfrac{1}{{{m_1}}} + \dfrac{1}{{{m_2}}}$.
B) ${m_1} + {m_2} = {m_3}$.
C) $\dfrac{4}{{{m_3}}} = \dfrac{1}{{{m_1}}} + \dfrac{1}{{{m_2}}}$.
D) $\dfrac{1}{{{m_1}}} + \dfrac{2}{{{m_2}}} = \dfrac{3}{{{m_3}}}$.

Answer 1

Hint:The tension in the string always acts away from the body so the tension on the string is always equal to the weight of the mass if the mass is in rest. The tension in the pulley is T then the tension in the string holding that pulley has double tension.

Complete step by step solution:
It is given in the problem that the masses ${m_1}$,${m_2}$ and ${m_3}$ are attached to a string and all the three masses are rest and then released also it is given that the mass ${m_3}$ will be at rest. The free body diagram will be.

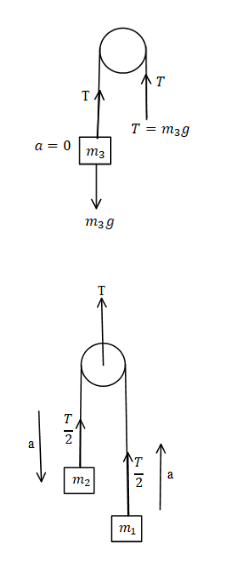
The tension in the string is equal to,
$ \Rightarrow T = 2{T_1}$………eq. (1)
The equation involving the mass ${m_1}$ is equal to,
$ \Rightarrow {T_1} - {m_1}g = {m_1}a$
Since, $T = 2{T_1}$
$ \Rightarrow \dfrac{T}{2} - {m_1}g = {m_1}a$………eq. (2)
The equation involving the mass ${m_2}$ is equal to,
$ \Rightarrow - {T_1} - {m_2}g = {m_2}a$
Since, $T = 2{T_1}$ therefore we get,
$ \Rightarrow - \dfrac{T}{2} + {m_2}g = {m_2}a$………eq. (3)
Dividing equation (2) by equation (3) we get,
$ \Rightarrow \dfrac{{\dfrac{T}{2} - {m_1}g}}{{ - \dfrac{T}{2} + {m_2}g}} = \dfrac{{{m_1}a}}{{{m_2}a}}$
$ \Rightarrow \dfrac{{\dfrac{T}{2} - {m_1}g}}{{ - \dfrac{T}{2} + {m_2}g}} = \dfrac{{{m_1}}}{{{m_2}}}$………eq. (4)
As the mass ${m_3}$ is at rest is given by,
$ \Rightarrow T = {m_3}g$………eq (5)
Replacing the value of equation (5) in equation (4) we get,
$ \Rightarrow \dfrac{{\dfrac{T}{2} - {m_1}g}}{{ - \dfrac{T}{2} + {m_2}g}} = \dfrac{{{m_1}}}{{{m_2}}}$
$ \Rightarrow \dfrac{{\left( {\dfrac{{{m_3}g}}{2}} \right) - {m_1}g}}{{ - \left( {\dfrac{{{m_3}g}}{2}} \right) + {m_2}g}} = \dfrac{{{m_1}}}{{{m_2}}}$
$ \Rightarrow \dfrac{{\left( {\dfrac{{{m_3}g - 2{m_1}g}}{2}} \right)}}{{\left( {\dfrac{{ - {m_3}g + 2{m_2}g}}{2}} \right)}} = \dfrac{{{m_1}}}{{{m_2}}}$
\[ \Rightarrow {m_2} \times \left( {\dfrac{{{m_3}g - 2{m_1}g}}{2}} \right) = {m_1} \times \left( {\dfrac{{ - {m_3}g + 2{m_2}g}}{2}} \right)\]
\[ \Rightarrow {m_2} \times \left( {{m_3}g - 2{m_1}g} \right) = {m_1} \times \left( { - {m_3}g + 2{m_2}g} \right)\]
\[ \Rightarrow {m_2}{m_3}g - 2{m_1}{m_2}g = - {m_3}{m_1}g + 2{m_1}{m_2}g\]
\[ \Rightarrow {m_2}{m_3} - 2{m_1}{m_2} = - {m_3}{m_1} + 2{m_1}{m_2}\]
\[ \Rightarrow {m_2}{m_3} + {m_3}{m_1} = 4{m_1}{m_2}\]
\[ \Rightarrow \dfrac{1}{{{m_1}{m_2}}}\left( {{m_2}{m_3} + {m_3}{m_1}} \right) = 4\]
\[ \Rightarrow \left( {\dfrac{{{m_3}}}{{{m_1}}} + \dfrac{{{m_3}}}{{{m_2}}}} \right) = 4\]
\[ \Rightarrow \dfrac{4}{{{m_3}}} = \dfrac{1}{{{m_1}}} + \dfrac{1}{{{m_2}}}\].
The relation of the masses${m_1}$,${m_2}$ and ${m_3}$ is equal to\[\dfrac{4}{{{m_3}}} = \dfrac{1}{{{m_1}}} + \dfrac{1}{{{m_2}}}\].

The correct answer for this problem is option C.

Note: The masses ${m_1}$ and ${m_2}$ will move with acceleration a but the acceleration of the mass ${m_3}$ will be given as zero therefore the tension is equal to the weight of the mass${m_3}$. It is advised to the students that the equation should be designed very carefully as the equations only will help us to solve this problem.