Question

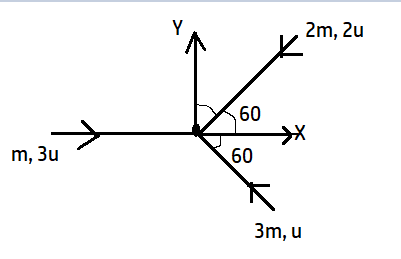
Three masses m, 2m and 3m are moving in the x-y plane with speeds 3u, 2u and u respectively as shown in the figure. The three masses collide at the same point at P and stick together. Find the velocity of the resulting mass?

A. \[\dfrac{u}{12}(\widehat{i}+\sqrt{3}\widehat{j})\]
B. \[\dfrac{u}{12}(\widehat{i}-\sqrt{3}\widehat{j})\]
C. \[\dfrac{u}{12}(-\widehat{i}-\sqrt{3}\widehat{j})\]
D. \[\dfrac{u}{12}(-\widehat{i}+\sqrt{3}\widehat{j})\]

Answer 1

Hint: This problem involves collision and there is no loss of energy during the collision. Also, there is no friction present on the ground. It makes a simple problem of energy conservation. We have to also consider the directions since it is of 2-dimension collision.

Complete step by step answer:
We will do this problem by separating components.
For X component:
For first mass:
Mass= m
Velocity= 3u
For second mass:
Mass= 2m
Velocity can be resolved as -2ucos60 = \[-2u\times \dfrac{1}{2}=-u\]
For third mass:
Mass= 3m
Velocity= -ucos60= \[-u\times \dfrac{1}{2}=-\dfrac{u}{2}\]
So, initial x component of linear momentum is \[{{m}_{1}}{{u}_{x1}}+{{m}_{2}}{{u}_{x2}}+{{m}_{3}}{{u}_{x3}}\]
\[\begin{align}
  & =3mu-2mu-\dfrac{3mu}{2} \\
 & \\
 & =mu-\dfrac{3mu}{2} \\
 & =\dfrac{-mu}{2} \\
\end{align}\]

For Y component:
For first mass:
Mass= m
Velocity= 0
For second mass:
Mass= 2m
Velocity can be resolved as -2usin60 = \[-2u\times \dfrac{\sqrt{3}}{2}=-u\sqrt{3}\]
For third mass:
Mass= 3m
Velocity= usin60= \[2u\times \dfrac{\sqrt{3}}{2}=u\sqrt{3}\]
So, initial y component of linear momentum is \[{{m}_{1}}{{u}_{y1}}+{{m}_{2}}{{u}_{y2}}+{{m}_{3}}{{u}_{y3}}\]
\[\begin{align}
& =0-2mu\sqrt{3}+3mu\sqrt{3} \\
& =mu\sqrt{3} \\
\end{align}\]
Now after the collision all the masses stick together, so total mass will be 6m
Let the x component of final velocity be \[{{V}_{x}}\]and y component be \[{{V}_{y}}\]
So, by law of conservation of linear momentum,
6m \[{{V}_{x}}\]= \[\dfrac{-mu}{2}\]
\[{{V}_{x}}=\dfrac{-u}{12}\]
For y component:
\[\begin{align}
& 6m{{V}_{y}}=mu\sqrt{3} \\
& {{V}_{y}}=\dfrac{u}{6}\sqrt{3} \\
\end{align}\]
So, the velocity of the resulting mass is
$
\dfrac{-u}{12}\widehat{i}-\dfrac{u}{12}\sqrt{3}\widehat{j} \\
\therefore \dfrac{u}{12}(-\widehat{i}-\sqrt{3}\overset\frown{j}) \\
$

So, the correct answer is “Option C”.

Note:
It is possible to resolve components only when the body is moving with constant velocity that is zero acceleration or with a constant value of acceleration.
If the body moves with varying acceleration then it is not possible to resolve the vectors.