Question

Three long, straight and parallel wires are arranged as shown in figure. The force
experienced by 10 cm length of wire $Q$ is

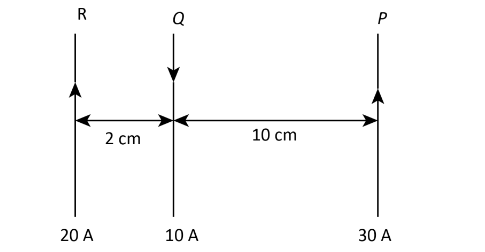
A. $1.4 \times {10^{ - 4}}\;{\rm{N}}$ toward the right
B. $1.4 \times {10^{ - 4}}\;{\rm{N}}$ towards the left
C. $2.6 \times {10^{ - 4}}\;{\rm{N}}$ toward the right
D. $2.6 \times {10^{ - 4}}\;{\rm{N}}$ toward the left

Answer 1

Hint: Find the magnetic field due to $R$ on Q and due to $P$on $Q$ and use this expression to find the force and when the current are in opposite direction in the straight conductor, then the force is repulsive in nature.

Formula used: The magnetic field due to infinitely long straight conductor: $B = \dfrac{{{\mu
_0}I}}{{2\pi a}}$

Complete step by step answer:
From the given question, we know that the current in wire $P.\;Q$ and $R$ are ${I_P} =
30\;{\rm{A}}$, ${I_Q} = 10{\rm{A}}$ and ${I_R} = 20\;{\rm{A}}$, the distance between the wire
$R\;$ and $Q$ is ${a_{RQ}} = 0.02\;{\rm{m}}$, the distance between the wire $P$ and $Q$ is
${a_{PQ}} = 0.1\;{\rm{m}}$ and the length of the wire $Q$ is $L = 0.1\;{\rm{m}}$
The magnetic field produced by wire $R$ at $Q$ is expressed as,
${B_{RQ}} = \dfrac{{{\mu _0}{I_R}}}{{2\pi {a_{RQ}}}}$
Since the force experienced by wire $Q$ is in left direction (repulsion) as the directions of the
current are anti parallel and it is calculated as,
$
{F_{RQ}} = {I_Q}L{B_{RQ}}\\
{F_{RQ}} = {I_Q}L\dfrac{{{\mu _0}{I_R}}}{{2\pi {a_{RQ}}}}
$

Similarly, the magnetic field produced by wire $P$ at $Q$ is expressed as,
${B_{PQ}} = \dfrac{{{\mu _0}{I_P}}}{{2\pi {a_{PQ}}}}$
Since the force experienced by wire $Q$ is in right direction (repulsion) as the directions of the
current are anti parallel and it is calculated as,
$
{F_{PQ}} = {I_Q}L{B_{PQ}}\\
{F_{PQ}} = {I_Q}L\dfrac{{{\mu _0}{I_P}}}{{2\pi {a_{PQ}}}}
$
The net force experienced by the wire $Q$ is calculated as,
$
F = {F_{RQ}} - {F_{PQ}}\\
= {I_Q}L\dfrac{{{\mu _0}{I_R}}}{{2\pi {a_{RQ}}}} - {I_Q}L\dfrac{{{\mu _0}{I_P}}}{{2\pi {a_{PQ}}}}\\
= \dfrac{{{I_Q}L{\mu _0}}}{{2\pi }}\left[ {\dfrac{{{I_R}}}{{{a_{RQ}}}} - \dfrac{{{I_P}}}{{{a_{PQ}}}}}
\right]\\
= \dfrac{{10 \times 0.1 \times 4\pi \times {{10}^{ - 7}}}}{{2\pi }}\left[ {\dfrac{{20}}{{0.02}} -
\dfrac{{30}}{{0.1}}} \right]\\
= 1.4 \times {10^{ - 4}}\;{\rm{N}}\;\;{\rm{towards}}\;{\rm{right}}
$

Thus, the force experienced by the wire $Q$ is $1.4 \times {10^{ - 4}}\;{\rm{N}}$ toward right
direction and option (A) is correct.

Note: Be careful while answering, because the formula for finite straight wire and infinite
straight are completely different.
When wire has finite length: \[B = \dfrac{{{\mu _0}I}}{{4\pi a}}\left( {\sin {\phi _2} + \sin {\phi
_1}} \right)\]
When wire has infinite length, ${\phi _1} = {\phi _2} = 90^\circ $: \[B = \dfrac{{{\mu _0}I}}{{2\pi
a}}\]
When wire has infinite length and point $P$ lies at near wire’s end, ${\phi _1} = 90^\circ
\;{\rm{and}}\;{\phi _2} = 0$:
\[B = \dfrac{{{\mu _0}I}}{{4\pi a}}\]