Question

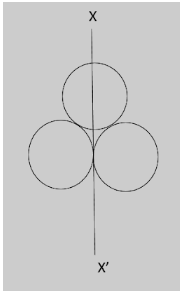
Three identical spherical shells, each of mass $ m $ and radius $ r $ are placed as shown in figure. Consider an axis $ XX' $ which is touching two shells and passing through the diameter of the third shell.
Moment of inertia of the system consisting of these three spherical shells about $ XX' $ axis is

(A) $ \dfrac{{16}}{5}m{r^2} $
(B) $ 4m{r^2} $
(C) $ \dfrac{{11}}{5}m{r^2} $
(D) $ 3m{r^2} $

Answer 1

Hint : The moment of inertia of a shell is given by $ \dfrac{2}{3}m{r^2} $ . We need to apply the parallel axis theorem to find the moment of inertia of the shell with respect to the axis tangent to the shell.

Complete step by step answer
It has been given that three shells of mass $ m $ and radius $ r $ are placed. An axis $ XX' $ is touching two shells of the three and passes through the diameter of the third shell.
Moment of inertia is defined as the quantity expressed by the body resisting angular acceleration which is the sum of the product of the mass of every particle with its square of a distance from the axis of rotation. In other words, it can be described as a quantity that decides the amount of torque needed for a specific angular acceleration in a rotational axis. Moment of Inertia is also known as the angular mass or rotational inertia. The SI unit of moment of inertia is $ {\text{kg }}{{\text{m}}^{\text{2}}} $ .
Moment of inertia is usually specified with respect to a chosen axis of rotation. It mainly depends on the distribution of mass around an axis of rotation. MOI varies depending on the axis that is chosen.
Moment of inertia of the shell with respect to an axis passing through its centre is $ \dfrac{2}{3}m{r^2} $ .
Thus, $ {I_{CM}} = {I_1} = \dfrac{2}{3}m{r^2} $ .
Parallel axis theorem states that-‘The moment of inertia of a body about an axis parallel to the body passing through its centre is equal to the sum of moment of inertia of body about the axis passing through the centre and product of mass of the body times the square of distance between the two axes.’
Mathematically, it can be written as, $ I = {I_C} + m{r^2} $
Moment of inertia of shell w.r.t. axis tangent to shell can be found using parallel axis theorem is
 $ {I_2} = {I_3} = {I_1} + m{r^2} $ .
 $ {{\text{I}}_{{\text{tangent}}}}{\text{ = }}{{\text{I}}_{{\text{CM}}}}{\text{ + m}}{{\text{r}}^{\text{2}}}{\text{ = }}\dfrac{{\text{5}}}{{\text{3}}}{\text{m}}{{\text{r}}^{\text{2}}} $ .
Thus, $ {I_2} = {I_3} = \dfrac{5}{3}m{r^2} $ .
Total moment of inertia with respect to the given axis- $ {I_{XX'}} = {I_1} + {I_2} + {I_3} $ .
Assigning the values of $ {I_2} $ and $ {I_3} $ in the equation,
 $ \dfrac{2}{3}m{r^2} + 2 \times \dfrac{5}{3}m{r^2} = \dfrac{{12}}{3}m{r^2} = 4m{r^2} $
So the correct answer is option B.

Note
Perpendicular axis theorem states that-‘For any plane body the moment of inertia about any of its axes which are perpendicular to the plane is equal to the sum of the moment of inertia about any two perpendicular axes in the plane of the body which intersect the first axis in the plane.’
Perpendicular axis theorem is used when the body is symmetric in shape about two out of the three axes if the moment of inertia about two of the axes are known the moment of inertia about the third axis can be found using the expression: $ {I_a} = {I_b} + {I_c} $ where $ a $ , $ b $ and $ c $ are the three mutually perpendicular axes.
Following are the applications of perpendicular axis theorem:
The calculation of the moment of inertia about the third axis is possible with the help of the perpendicular axis theorem.
The moment of inertia for three-dimensional objects can be determined by using the perpendicular axis theorem.