Question

Three identical spheres each of radius R are placed touching each other on a horizontal table as shown in the figure.

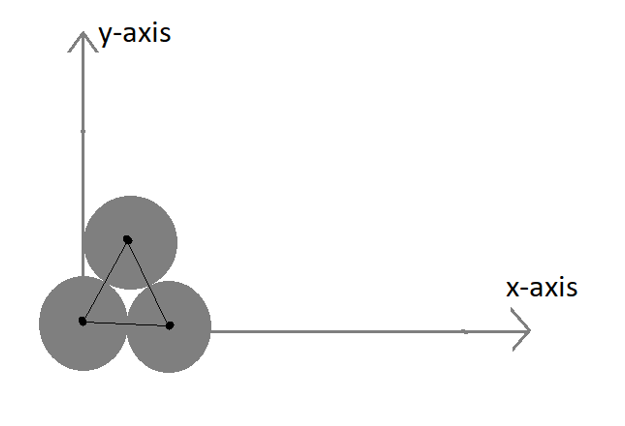
 The coordinates of the Centre of mass are:
A. $(R,R)$
B. $(0,0)$
C. $(\dfrac{R}{2},\dfrac{R}{2})$
D. $(R,\dfrac{R}{{\sqrt 3 }})$

Answer 1

Hint:The rigid body is defined as the collection of particles such that the distance from any two points remains constant during the motion of the body. A rigid body can be of any shape so here introduced the concept of center of mass. The Center of mass is that point where the effective weight of the body is concentrated. The Center of mass is that point where any uniform force acts on the body. The Center of mass makes it easy to solve the mechanics' problems of any random-shaped body.


Complete step by step solution:
We have to find the center of mass coordinates of the given figure.
The coordinates of the spheres are $\left( {0,0} \right)$, $\left( {2R,0} \right)$ and $\left( {R,\sqrt 3 R} \right)$.
The formula to calculate the x-coordinate of the center of mass is given below.
${x_{com}} = \dfrac{{{m_1}{x_1} + {m_2}{x_2} + {m_3}{x_3}}}{{{m_1} + {m_2} + {m_3}}}$
Let us substitute the values.
${x_{com}} = \dfrac{{M \times 0 + M \times 2R + M \times R}}{{M + M + M}} = \dfrac{{3MR}}{{3M}}$
${x_{com}} = R$
Similarly, the formula to calculate the y-coordinate of the center of mass is given below.
${y_{com}} = \dfrac{{{m_1}{y_1} + {m_2}{y_2} + {m_3}{y_3}}}{{{m_1} + {m_2} + {m_3}}}$
Let us substitute the values.
${y_{com}} = \dfrac{{M \times 0 + M \times 0 + M \times \sqrt 3 R}}{{M + M + M}} = \dfrac{{\sqrt 3 MR}}{{3M}}$
${y_{com}} = \dfrac{R}{{\sqrt 3 }}$
Therefore, the coordinates of the center of mass are $\left( {R,\dfrac{R}{{\sqrt 3 }}} \right)$.
Hence, option (D) $\left( {R,\dfrac{R}{{\sqrt 3 }}} \right)$ is correct.

Note:
Always find the position coordinates of the different points of the combination.
The Center of mass is a hypothetical point, where the entire mass of the body is assumed to be concentrated.
When we apply force at the center of mass of the body, it moves as if it is a point mass.
The Center of mass does not rotate itself. It makes a parabolic path, as a point mass.
The Center of mass can also exist outside of the body, for example, horseshoe.