Question

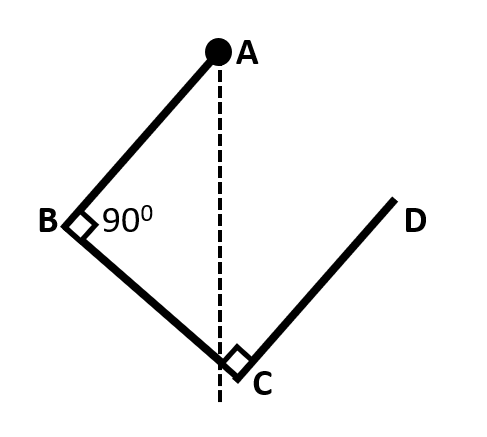
Three identical rods are hinged at point A as shown. The angle made by rod AB with the vertical is:

$\begin{align}
  & (A){{\tan }^{-1}}\left( \dfrac{1}{\sqrt{3}} \right) \\
 & (B){{\tan }^{-1}}\left( \dfrac{3}{4} \right) \\
 & (C){{\tan }^{-1}}(1) \\
 & (D){{\tan }^{-1}}\left( \dfrac{4}{3} \right) \\
\end{align}$

Answer 1

Hint: At equilibrium, the center of mass of the entire three rod system must lie at a point somewhere along the vertical line that is passing through A. This is because, at equilibrium the net torque due to the weight of the system should be zero about any axis. So, about this vertical axis too, the net torque should be zero.

Complete step-by-step solution:
Let us first calculate the center of mass of the two parallel rods. Assuming the length of each rod to be ‘l’ and its mass to be ‘m’. The center of mass of two parallel rods will lie at their mid-point at a distance of $\dfrac{l}{2}$ downwards along their length. Let us understand this with the help of following diagram:

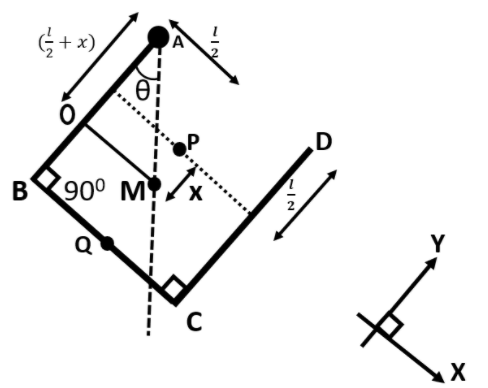
Here, P is the COM of rods AB and CD. And Q is the COM of rod BC. The combined COM of P and Q will give us the COM of the entire three rod system.
Thus from the above diagram it is clear that:
$\Rightarrow {{X}_{COM}}=\dfrac{l}{2}$
And,
$\Rightarrow {{Y}_{COM}}=x\text{ }(\text{measured from P})$
Thus, ‘x’ can be calculated as follows:
$\begin{align}
  & \Rightarrow x=\dfrac{m\times \dfrac{l}{2}+2m\times 0}{m+2m} \\
 & \therefore x=\dfrac{l}{6} \\
\end{align}$
Now, let the angle made by the vertical line with the rod AB be equal to $\theta $. Then, in triangle AOM, we can write that:
$\Rightarrow \tan \theta =\dfrac{OM}{OA}$ [Let this expression be equation number (1)]
Where,
$\Rightarrow OM=\dfrac{l}{2}$
And,
$\begin{align}
  & \Rightarrow OA=\dfrac{l}{2}+x \\
 & \Rightarrow OA=\dfrac{l}{2}+\dfrac{l}{6} \\
 & \therefore OA=\dfrac{2l}{3} \\
\end{align}$
Thus, putting these values in equation number (1), we get:
$\begin{align}
  & \Rightarrow \tan \theta =\dfrac{\dfrac{l}{2}}{\dfrac{2l}{3}} \\
 & \Rightarrow \tan \theta =\dfrac{3}{4} \\
 & \therefore \theta ={{\tan }^{-1}}\left( \dfrac{3}{4} \right) \\
\end{align}$
Hence, the angle made by rod AB with the vertical comes out to be ${{\tan }^{-1}}\left( \dfrac{3}{4} \right)$.
Hence, option (B) is the correct option.

Note: In problems like these, it is always important to analyze the basic concepts that are to be applied. If we wouldn’t have been able to deduce the fact that the COM of the entire system lies on the vertical axis, we would have never been able to get our answer. And, this visualization of facts comes only after practicing a lot of problems like these.