Question

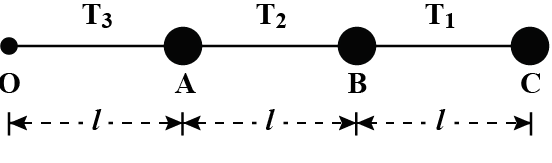
Three identical particles are joined together by a thread as shown in figure. All the three particles are moving in a circular path in a horizontal plane. If the velocity of the outermost particle is \[{v_0}\], then the ratio of tensions in the three sections of the string is:

Answer 1

Hint: In this question use the concept of centrifugal force i.e. a force, arising from the body’s inertia, which appears to act on a body moving in a circular path and is directed away from the centre around which the body is moving.
Formula used :- ${T_C} = m{w^2}\left( {3l} \right)$ the centrifugal force which is given by $m{w^2}2r$ where is radius and our case there is length i.e. $l$.

Complete step-by-step solution -
According to the question there are three identical particles that are joined together by a thread and all the three particles are moving in circular path in a horizontal plane , so we have to find the ratio of tensions in the three sections of the string when the velocity of the outermost particle is ${v_0}$.
Hence, angular velocity $w$ is same for all
$ {T_C} = m{w^2}\left( {3l} \right) \\
  {T_B} = {T_C} + m{w^2}\left( {2l} \right) = m{w^2}\left( {5l} \right) \\
  {T_A} = {T_B} + m{w^2}\left( l \right) = m{w^2}\left( {6l} \right) \\
  \therefore {T_C}:{T_B}:{T_A}:\;:\;3:5:6 \\ $

Note: In such types of questions we use the concept of circular motion in horizontal paths . The horizontal simulates the motion of a mass on a rigid rod that is moving along a horizontal – oriented circular path. It also explores the relationship between the inward force acting on an object travelling in uniform circular motion and the object’s mass, path radius , and speed.