Question

Three horses are tethered with 7-meter-long ropes at the three corners of a triangular field having sides 20 m, 34 m, and 42 m. Find the area of the field which can be grazed by the horses and the area of the plot which remains ungrazed.

Answer 1

Hint:We know that the sum of all the angles of the triangle is $ 180{}^\circ $ and the length of the rope of each horse is 7 meters. Hence, they will form the arc of equal radius. And, the sum of all the angles formed of the respective arc at each corner by the horses is also equal to $ 180{}^\circ $ . So, the total area grazed by all the three horses will be equivalent to the area of the semicircle which is of radius 7 m. Area of each arc will be given by $ area=\dfrac{\theta }{360{}^\circ }\times \pi \times {{r}^{2}} $ and to find area of ungrazed part we will subtract the area of ungrazed part from area of the triangle by using formula $ area=\sqrt{s\left( s-a \right)\left( s-b \right)\left( s-c \right)} $
where s is a semi-perimeter of the triangle $ s=\dfrac{a+b+c}{2} $ .

Complete step-by-step answer:
We know from the question that the length of the rope of each horse is equal to 7 m. Hence, the maximum area of the field which can be grazed by each horse will be equal to the sum of the area of the sector which each horse will make at each corner of the field. Since, the angle of each sector will be equal to the angle made by two respective sides of the triangle.

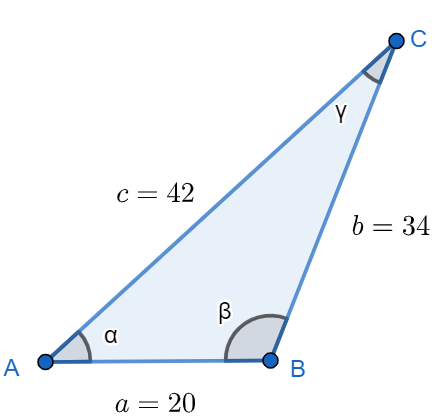
Let us assume that $ \alpha $ , $ \beta $ and $ \gamma $ are the angles made by the sides of the triangle.
So, $ \alpha +\beta +\gamma =180{}^\circ $
So, the angles made by each of the respective arcs are also $ \alpha $ , $ \beta $ and $ \gamma $ .
Here, radius of each arc = 7 m
So, the total area of the field which is grazed = Area of the arc made by the horse at A + Area of the arc made by the horse at B + area of the arc made by the horse at C.
 $ =\dfrac{\alpha }{360{}^\circ }\times \pi \times {{\left( 7 \right)}^{2}}+\dfrac{\beta }{360{}^\circ }\times \pi \times {{\left( 7 \right)}^{2}}+\dfrac{\gamma }{360{}^\circ }\times \pi \times {{\left( 7 \right)}^{2}}{{m}^{2}} $
 $ =\dfrac{(\alpha +\beta +\gamma )}{360{}^\circ }\times \pi \times 7{{m}^{2}} $
Since, $ \alpha +\beta +\gamma =180{}^\circ $
 $ =\dfrac{180{}^\circ }{360{}^\circ }\times \pi \times {{(7)}^{2}}{{m}^{2}} $
 $ =\pi \times \dfrac{49}{2}{{m}^{2}} $
 $ =76.969{{m}^{2}} $
Hence, the total area grazed by the horse is $ 76.969{{m}^{2}} $ . Now, we find the area of the triangle:
So, area of the triangle $ \Delta ABC $ is given by:
 $ area=\sqrt{s\left( s-a \right)\left( s-b \right)\left( s-c \right)} $ where, $ s=\dfrac{a+b+c}{2} $
So, $ s=\dfrac{20+34+42}{2} $ = $ \dfrac{96}{2}=48m $
So, area of triangle is $ \sqrt{48\left( 48-20 \right)\left( 48-34 \right)\left( 48-42 \right)}{{m}^{2}} $
 $ =\sqrt{48\times 28\times 14\times 6}{{m}^{2}} $
 $ =336{{m}^{2}} $
Hence, the area of the ungrazed part = Area of triangle – Area of the grazed part $ =336{{m}^{2}}-76.969{{m}^{2}} $
 $ =259.031{{m}^{2}} $
Hence, area of the field which can be grazed is equal to $ 76.969{{m}^{2}} $ and the area of the ungrazed part is equal to $ 259.031{{m}^{2}} $ .

Note: Most of the students make mistakes while calculating the area of each sector, as they forgot to mention angles made by each sector at the corner of the triangle. And, we are also required to check that the length of each side of the triangle should not be less than twice the length of the rope and if this happens then there will be some common area which will be grazed by more than one horse and hence we will not be able to calculate the area of the field which is being grazed and left ungrazed by the horses by the above method.