Question

Three girls Reshma, Salma and Mandeep are playing a game by standing on a circle of radius 5cm drawn in the park. Reshma throws a ball to Salma, Salma to Mandeep, Mandeep to Reshma. If the distance between Salma and Reshma, and between Salma and Mandeep is 6cm each. What is the distance between Reshma and Mandeep?

Answer 1

Hint: First draw a suitable diagram with the given information. Now, use Pythagoras in triangles formed inside the circle. Use congruence of triangles wherever required. Pythagoras theorem can be given as ${{\left( \text{hypotenuse} \right)}^{\text{2}}}\text{=}{{\left( \text{base} \right)}^{\text{2}}}\text{+}{{\left( \text{perpendicular} \right)}^{\text{2}}}$.

Complete step-by-step answer:

Here, it is given that Reshma, Salma and Mandeep are standing on a circle of radius 5cm and the distance between Salma and Reshma and between Salma and Mandeep is 6cm each and hence, we need to determine distance between Reshma and Mandeep.
Let us suppose the distance between Reshma and Mandeep be ‘x’ cm.
Now, we can show the given information in a diagram as

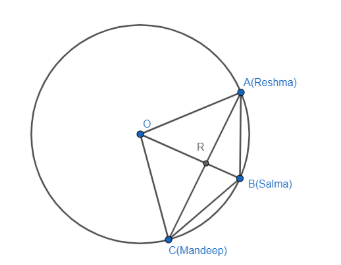
Here we know that
OA= OC = OB = radius = 5cm
AB = BC = 6cm
AC = distance ‘x’ representing distance between Reshma and Mandeep
Now in $\text{ }\!\!\Delta\!\!\text{ OCB}$ and $\text{ }\!\!\Delta\!\!\text{ OAB}$
0A = OC = radius = 5cm
BC = BA = 6cm (given)
OB = OB = 5cm (common)
Hence, $\text{ }\!\!\Delta\!\!\text{ OCB}\cong \Delta \text{OAB}$by SSS criteria
So, by CPCT, we have
 $\begin{align}
  & \angle COB=\angle AOB \\
 & \angle COR=\angle AOR \\
\end{align}$………………….. (i)
Now, coming to the triangles $\Delta OCR$ and $\Delta OAR$, we have
OA = OC = radius = 5cm
OR =OR (common)
$\angle COR=\angle AOR$ (by equation (i))
Hence, $\Delta OCR\cong \Delta OAR$
And hence, we get by CPCT
CR = AR and $\angle ORC=\angle ORA$
Now, as we know the angle formed on a line at a point is ${{180}^{\circ }}$ (straight line), so $\angle ORC,\angle ORA$ are forming a linear pair on AC. So, the sum of them will be ${{180}^{\circ }}$ . So, we get
$\angle ORC+\angle ORA={{180}^{\circ }}$
As both the angles are equal by CPCT so, we can rewrite the above equation as
$\begin{align}
  & \angle ORC+\angle ORC={{180}^{\circ }} \\
 & 2\angle ORC={{180}^{\circ }} \\
 & \angle ORC={{90}^{\circ }} \\
\end{align}$
And hence
$\angle ORA={{90}^{\circ }}$
Hence, OR is acting as an altitude for $\Delta OAC$ at point R.
Now, we know that altitude divides the side in equal lengths in an isosceles triangle. As $\Delta COA$ is an isosceles triangle as OC = OA (radius), so $OR\bot AC$ .
Hence, we get

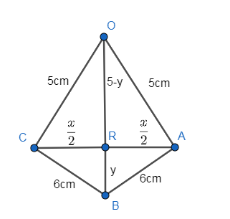
Let distance BR be ‘y’ cm, so, distance OR be ‘5 - y’ cm as OB is radius (5cm).
Now, apply Pythagora's theorem in $\Delta \text{ORA}$ and $\Delta ARB$.
So, from $\Delta \text{ORA}$, we get
${{\left( \dfrac{x}{2} \right)}^{2}}+{{\left( 5-y \right)}^{2}}={{5}^{2}}$ …………….. (ii)
From $\Delta ARB$, we get
${{\left( \dfrac{x}{2} \right)}^{2}}+{{\left( y \right)}^{2}}={{\left( 6 \right)}^{2}}$ ………………… (iii)
Now, we can subtract equation (ii) and (iii), hence, we get
$\begin{align}
  & \left( {{\left( \dfrac{x}{2} \right)}^{2}}+\left( {{y}^{2}} \right) \right)-\left( {{\left( \dfrac{x}{2} \right)}^{2}}+{{\left( 5-y \right)}^{2}} \right)={{6}^{2}}-{{5}^{2}} \\
 & \Rightarrow {{\left( \dfrac{x}{2} \right)}^{2}}+{{y}^{2}}-{{\left( \dfrac{x}{2} \right)}^{2}}-{{\left( 5-y \right)}^{2}}=36-25 \\
 & \Rightarrow {{y}^{2}}-{{\left( 5-y \right)}^{2}}=36-25=11 \\
\end{align}$

Now, use ${{\left( a-b \right)}^{2}}={{a}^{2}}+{{b}^{2}}-2ab$, hence, we get
$\begin{align}
  & {{y}^{2}}-\left( 25+{{y}^{2}}-10y \right)=11 \\
 & 10y-25=11 \\
 & 10y=36 \\
 & \Rightarrow y=3.6...........(iv) \\
\end{align}$
Now, put value of ‘y’ from the equation (iv) in equation (iii), we get
$\begin{align}
  & {{\left( \dfrac{x}{2} \right)}^{2}}+{{\left( 3.6 \right)}^{2}}={{6}^{2}} \\
 & {{\left( \dfrac{x}{2} \right)}^{2}}={{6}^{2}}-{{\left( 3.6 \right)}^{2}} \\
\end{align}$
Now, use the algebraic identity given as ${{a}^{2}}-{{b}^{2}}=\left( a-b \right)\left( a+b \right)$ in the above equation, we get
$\begin{align}
  & \dfrac{{{x}^{2}}}{{{2}^{2}}}=\left( 6-3.6 \right)\left( 6+3.6 \right) \\
 & {{x}^{2}}=2.4\times 4\times 9.6 \\
 & {{x}^{2}}=9.6\times 9.6 \\
\end{align}$
Taking square root on both sides, we get
x = 9.6cm
Therefore, the distance between Reshma and Mandeep is 9.6cm.

Note: Another approach for the question would be that we can apply cosine formula for calculating cos (COB). Cosine formula is given as
$\cos \theta =\dfrac{{{b}^{2}}+{{c}^{2}}-{{a}^{2}}}{2bc}$
Here $\theta $is the angle between side b and c in a triangle.
Now in $\Delta OCR$ take $\sin \left( \angle COR \right)$ to get the length CR. So, this can be another approach.
One can draw perpendiculars to BC and AB and can equate the area of $\Delta OBC$ as
$\dfrac{1}{2}\times OM\times BC=\dfrac{1}{2}\times OR\times RC$
Here OM is perpendicular on BC. This can be another approach for the given question.
One can go wrong with the solution if he/she takes the distance between the girls on the circumference of the circle i.e. he/she may take the distance of arc AB and arc BC as 6cm which is wrong. Given distances are the direct distances between girls.