Question

Three forces of 3N, 2N and 1N act on a particle as shown in the figure.

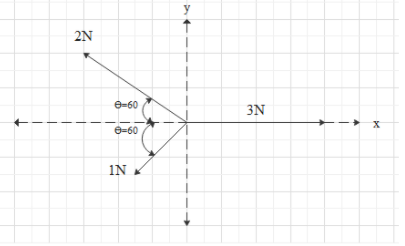
Obtain the net force along the x axis
A. ${F_x} = 2N$
B. ${F_x} = \dfrac{1}{2}N$
C. ${F_x} = \dfrac{3}{2}N$
D. ${F_x} = \dfrac{5}{2}N$

Answer 1

Hint: These kind of questions to be solved by resolution of vectors. Every vector can be resolved into two components along the perpendicular axes. Here perpendicular axes are the x axis and the y axis. We have the angle made by the vector with x axis hence we can resolve the vector components along the x axis and finally add them to get net force along x axis.

Complete answer:

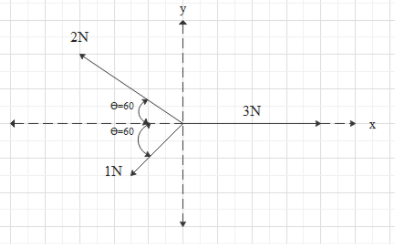
In the given question
2N vector is making ${60^0}$ with the x axis and 1N vector is making same ${60^0}$ with the x axis and 3N vector is along the x axis
Now component of 2N vector along x axis is $2\cos ({60^0})$ in negative x axis direction
Let it be A = $ - 2\cos ({60^0}) = - 2 \times \dfrac{1}{2} = - 1N$
Now component of 1N vector along x axis is $1\cos ({60^0})$ in negative x axis direction
Let it be B = $ - 1\cos ({60^0}) = - 1 \times \dfrac{1}{2} = \dfrac{{ - 1}}{2}N$
Now component of 3N vector along x axis is $3\cos ({0^0})$ in positive x axis direction
Let it be C = $3\cos ({0^0}) = 3 \times 1 = 3N$
Now adding all the components along x axis we get
$A + B + C = - 1 + \dfrac{{ - 1}}{2} + 3 = \dfrac{3}{2}$

Hence the answer would be option C.

Additional information:
We can resolve a vector along any two perpendicular axes. But standard reference axes we take are x and y axes in two dimensions and x,y,z axes in three dimensions.

Note:
Generally the angle we take with reference to the x-axis must be taken in an anticlockwise direction to get the correct answer. Here in case of 2N and 1N vectors we took in the clockwise direction and we compensated it later by multiplying that x component with negative sign. If angle is already taken anticlockwise then no need to multiply with a negative sign.