
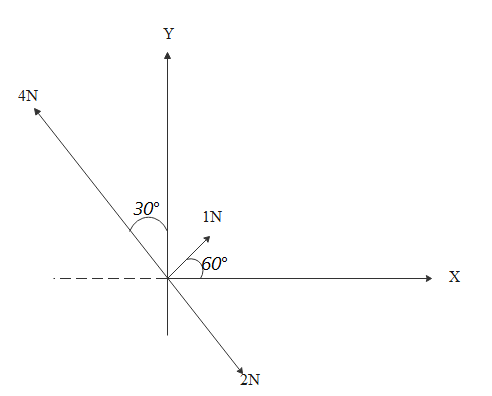
Three forces acting on a body are shown in fig. To have the resultant force only along the y-direction, the magnitude of the minimum additional force needed is
A. $\dfrac{{\sqrt 3 }}{4}N$
B. $\sqrt 3 N$
C. $0.5N$
D $1.5N$

Answer
568.2k+ views
Hint: This can be solved by the resolution of vectors along the coordinate axes. We are asked to find the magnitude of minimum force required so that resultant force will be along y direction only. we will find the horizontal components of all forces and add the required force to make resultant along x axis as zero.
Complete answer:
Basically physical quantities can be divided into vectors and scalars. Scalars have magnitude that means the value. But the vector has both magnitude and direction. For any vector we can denote in the form of magnitude and the direction where that vector is pointing.
In order to represent a vector first we should have one coordinate system. There will be one reference point called origin. There will be 2 reference axes if we consider only a two dimensional plane and there will be three reference axes if we consider three dimensional space.
All these axes will be mutually perpendicular. The point of intersection of these axes will be the origin.
Let $\mathop r\limits^ \to $ be the vector and this vector will have both magnitude and direction. Magnitude of vector will be $\left| r \right|$ while the direction of this vector will be along $\mathop r\limits^ \wedge $. $\mathop r\limits^ \wedge $ is called as unit vector
From the formula $\mathop r\limits^ \to = \left| r \right|\mathop r\limits^ \wedge $ we get unit vector as $\dfrac{{\mathop r\limits^ \to }}{{\left| r \right|}} = \mathop r\limits^ \wedge $.
The given forces are given below.
We will resolve the given vectors along the unit vector X. i.e along the x axis.
Component of 1N along x axis will be $1\cos 60 = 1(\dfrac{1}{2}) = 0.5$
Component of 2N along x axis will be $2\cos 60 = 2(\dfrac{1}{2}) = 1$
Component of 4N along x axis will be $ - 4\cos 60 = - 4(\dfrac{1}{2}) = - 2$
Total force along positive x axis is 1.5N and along negative x axis is 2N so the additional of 0.5N is required along the positive x axis to make the net force zero along the axis.
Hence option C will be the answer.
Note:
There is no need to resolve the vectors along y axis because we should make them resultant along x axis zero. This has nothing to do with y components. Whatever may be the net force along the y axis we don’t need to worry about it because to get the minimum force required we should add force in the x axis only.
Complete answer:
Basically physical quantities can be divided into vectors and scalars. Scalars have magnitude that means the value. But the vector has both magnitude and direction. For any vector we can denote in the form of magnitude and the direction where that vector is pointing.
In order to represent a vector first we should have one coordinate system. There will be one reference point called origin. There will be 2 reference axes if we consider only a two dimensional plane and there will be three reference axes if we consider three dimensional space.
All these axes will be mutually perpendicular. The point of intersection of these axes will be the origin.
Let $\mathop r\limits^ \to $ be the vector and this vector will have both magnitude and direction. Magnitude of vector will be $\left| r \right|$ while the direction of this vector will be along $\mathop r\limits^ \wedge $. $\mathop r\limits^ \wedge $ is called as unit vector
From the formula $\mathop r\limits^ \to = \left| r \right|\mathop r\limits^ \wedge $ we get unit vector as $\dfrac{{\mathop r\limits^ \to }}{{\left| r \right|}} = \mathop r\limits^ \wedge $.
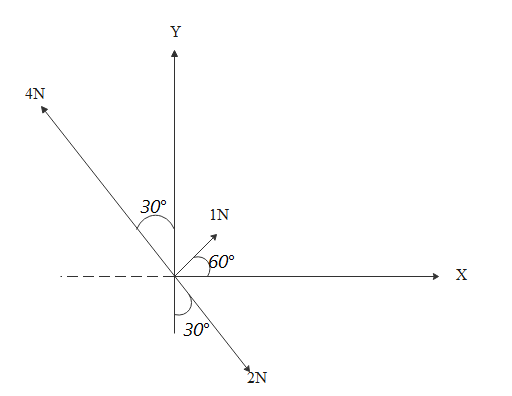
The given forces are given below.
We will resolve the given vectors along the unit vector X. i.e along the x axis.

Component of 1N along x axis will be $1\cos 60 = 1(\dfrac{1}{2}) = 0.5$
Component of 2N along x axis will be $2\cos 60 = 2(\dfrac{1}{2}) = 1$
Component of 4N along x axis will be $ - 4\cos 60 = - 4(\dfrac{1}{2}) = - 2$
Total force along positive x axis is 1.5N and along negative x axis is 2N so the additional of 0.5N is required along the positive x axis to make the net force zero along the axis.
Hence option C will be the answer.
Note:
There is no need to resolve the vectors along y axis because we should make them resultant along x axis zero. This has nothing to do with y components. Whatever may be the net force along the y axis we don’t need to worry about it because to get the minimum force required we should add force in the x axis only.
Recently Updated Pages
Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Trending doubts
There are 720 permutations of the digits 1 2 3 4 5 class 11 maths CBSE

Discuss the various forms of bacteria class 11 biology CBSE

Explain zero factorial class 11 maths CBSE

What organs are located on the left side of your body class 11 biology CBSE

Draw a diagram of nephron and explain its structur class 11 biology CBSE

How do I convert ms to kmh Give an example class 11 physics CBSE




