Question

Three forces A, B, C act at a point are in equilibrium. The ratio of the angle between A and B; B and C; and A and C is 1:2:3. Then, A:B:C is
A. \[1:\dfrac{{\sqrt 3 }}{2}:\dfrac{1}{2}\]
B. \[\dfrac{1}{2}:\dfrac{{\sqrt 3 }}{2}:1\]
C. \[1:\dfrac{1}{2}:\dfrac{1}{3}\]
D. \[1:\dfrac{1}{{\sqrt 2 }}:\dfrac{1}{{\sqrt 3 }}\]
E. None of these.

Answer 1

Hint: To calculate the value of A:B:C we have to figure out the angles between each force. Then after we will apply Lamis's theorem for mechanical equilibrium to get the required ratio.
Complete step-by-step answer:
Let α,β and γ are the angles between the forces A, B and C
as seen in the figure.

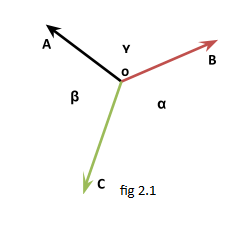
According to question, \[\gamma {\text{ }}:{\text{ }}\alpha {\text{ }}:{\text{ }}\beta \; = {\text{ }}1{\text{ }}:{\text{ }}2{\text{ }}:{\text{ }}3\]
Calculating the values for\[\alpha ,{\text{ }}\beta {\text{ }}and{\text{ }}\gamma \].
Let the required multiple of angles be\[x\].
So, \[\gamma = x,{\text{ }}\alpha = 2x\;and\;\beta = 3x\]
Since all these angles are making a complete angle at point O.
Therefore,
\[\alpha + \beta {\text{ }} + \gamma = {360^0}\]
\[\begin{gathered}
   \Rightarrow x + 2x + 3x = {360^0} \\
   \Rightarrow 6x = {360^0} \\
   \Rightarrow x = {60^0} \\
\end{gathered} \]
We get, \[\gamma = {60^0},\alpha = {120^0}{\text{ and }}\beta = {180^0}\]
Under equilibrium condition:-
\[ \Rightarrow \dfrac{{\text{A}}}{{{\text{sin12}}{0^0}}}{\text{ = }}\dfrac{{\text{B}}}{{{\text{sin18}}{0^0}}}{\text{ = }}\dfrac{{\text{C}}}{{{\text{sin}}{{60}^0}}}\]

Hence, Option (E) is the correct answer.


Note:In order to tackle such types of questions we should have to practice more questions based on the concept of the mechanical equilibrium state of a system. Since in mechanical equilibrium, the value of net torque and the net applied force is zero but we use Lami's theorem only for a mechanical system possessing state of equilibrium with zero value of net applied force.