Question

Three equal circles each of radius $r$ touch one another. The radius of the circle which touching by the three given circles internally is
 A. $\left( 2+\sqrt{3} \right)r$
B. $\dfrac{\left( 2+\sqrt{3} \right)}{\sqrt{3}}r$
C. $\dfrac{\left( 2-\sqrt{3} \right)}{\sqrt{3}}r$
D. $\left( 2-\sqrt{3} \right)r$

Answer 1

Hint: To solve this question, first of all we will draw the diagram according to the given condition in the question. Then, we will observe that the triangle drawn by the joint of the centre of all circles is an equilateral triangle and the intersecting points of all the triangles are the midpoint of the sides of the triangle. The line joint to the mid points that intersects one another in a point will be incenter, circumcenter and orthocenter and it will be the center of the small circle. So, the point divides the height of the equilateral triangle in ratio $2:1$. So, we will take the $\dfrac{2}{3}$ rd height of the circle. Then, we will subtract the radius of one circle to find the radius of a small circle.

Complete step by step answer:
Since, we will draw three circles of radius $r$touched by one another name $a,b$ and $c$. Then, we will draw the small circle touching by the three circles internally named $d$. Now, By joining the centre of the circles, we will get an equilateral triangle of side $2r$ and the midpoint of the sides is the intersecting point of circles also. Now, we will join the midpoints of all sides to the respective front head and will find that these lines intersect one another at a point and that point is the centre of a small circle circle.

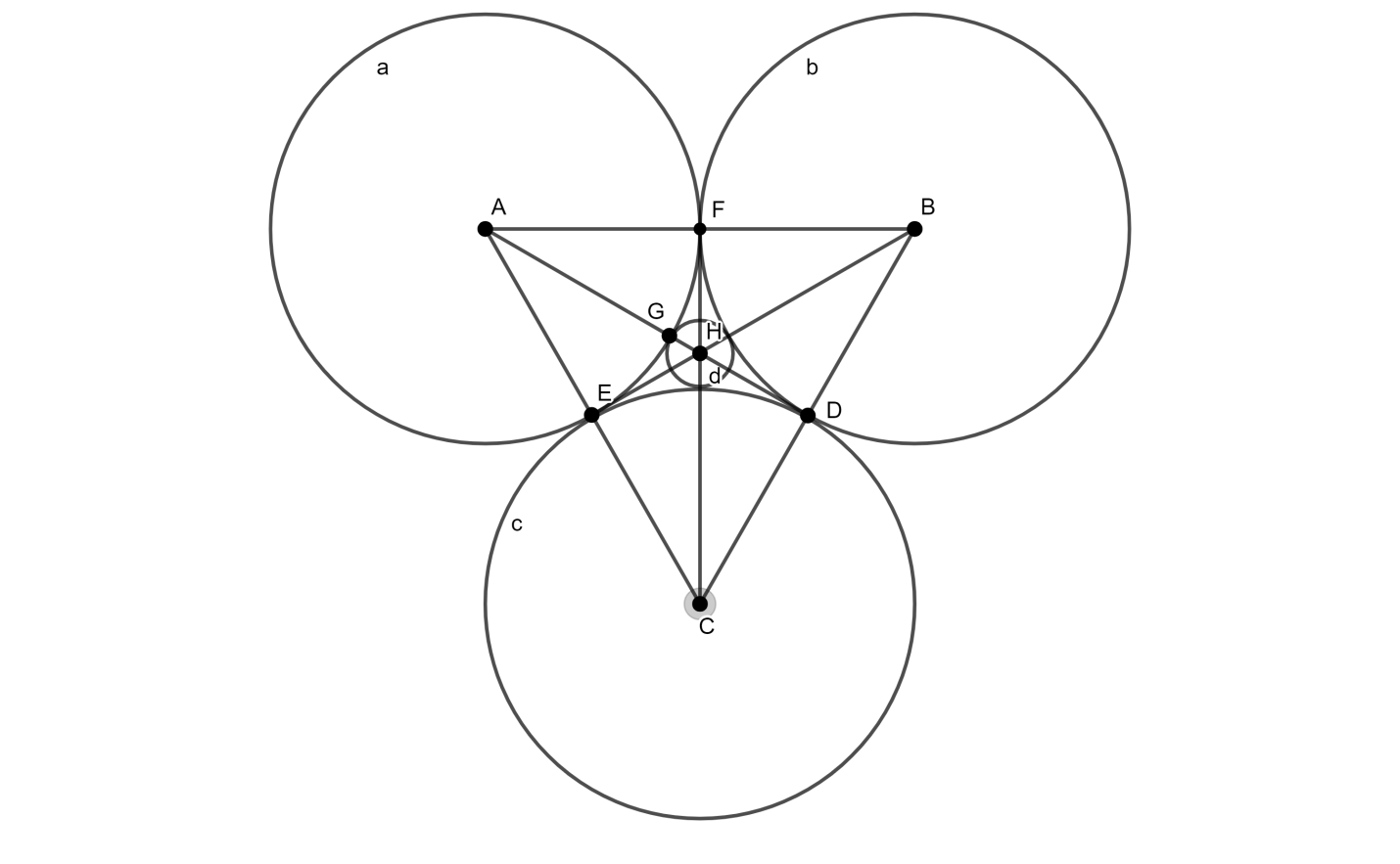Now, from the above diagram, we can clearly see that $\Delta ABC$ is an equilateral triangle and $D,E$ and $F$ are the midpoint of sides $BC,CA$ and $AB$ respectively. The line joining the points $A$ and $D$ is the height of the equilateral triangle.
Here, we will calculate the height of the equilateral triangle $\Delta ABC$. Since, the length of the side of the equilateral triangle $\Delta ABC$ is $2r$. So, the height of equilateral triangle:
$\Rightarrow AD=\dfrac{\sqrt{3}}{2}\times side$
Here, we will substitute $2r$ for side as:
$\begin{align}
  & \Rightarrow AD=\dfrac{\sqrt{3}}{2}\times 2r \\
 & \Rightarrow AD=\sqrt{3}r \\
\end{align}$
Since, the intercenter, circumcenter, centroid and orthocenter of the equilateral triangle is the same point and in this diagram that point is $H$ that is also the centre of the small circle $d$. It is also known that the centroid divides the height into two parts in the ratio \[2:1\].
So, we will have the ratio of the height as:
$\Rightarrow AH:HD=2:1$
Here, we will calculate the length of $AH$ by using the ratio as:
$\Rightarrow AH=\dfrac{2}{3}\times AD$
Now, we will substitute $\sqrt{3}r$ for $AD$ as:
$\Rightarrow AH=\dfrac{2}{3}\times \sqrt{3}r$
Here, we will simplify the above step by required methods and will have the length of line $AH$ as:
$\Rightarrow AH=\dfrac{2r}{\sqrt{3}}$
We can clearly see that the radius of small circle $d$ is $GH$ and we can write it as:
$\Rightarrow GH=AH-AG$
It can be clearly observed that $AG$ is the radius of circle $a$. So, the length of $AG$ is $r$. Here, we can substitute the obtained value of $AH$ and $r$ for $AG$ in the above expression as:
$\Rightarrow GH=\dfrac{2r}{\sqrt{3}}-r$
Now, we will simplify the above step as:
$\begin{align}
  & \Rightarrow GH=\dfrac{2r-\sqrt{3}r}{\sqrt{3}} \\
 & \Rightarrow GH=\dfrac{\left( 2-\sqrt{3} \right)r}{\sqrt{3}} \\
\end{align}$
So, the correct answer is “Option C”.

Note: Incenter: This is the point in which the line of bisector of all the angles of a triangle intersects.
Circumcenter: This is the intersecting point of the perpendicular line on the sides of a triangle.
Centroid: this is the intersecting point of medians of a triangle.
Orthocenter: This is the point of intersection of heights of a triangle.