Question

Three cubes are joined end to end forming a cuboid. If the side of a cube is $2cm$. Find the dimension of the cuboid thus obtained.

Answer 1

Hint: In this question, three cubes are joined end to end. So as cubes are joined end to end, the height and the breadth will remain the same, and length will change. The length of the cuboid will be the sum of all three cube’s length.

Complete step-by-step answer:
Let the side of the cube is $l$ cm. Since the cubes are the same, the length of all cubes will be $l$ cm.
We can show three cubes as below.

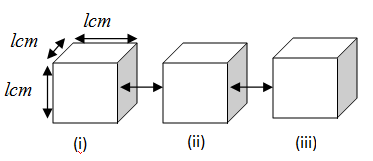
By adding all three cubes end to end, we can show it as below.

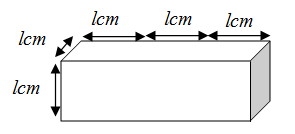
From the above diagrams, we can clearly see that by joining all three cubes end to end, there is no effect on height and breadth; but the length of cuboid so obtained is the sum of length of all three cubes.
As given in the question, the side of the cube is $2cm$, so \[l=2cm\].
Let the length, breadth and height of the cuboid is ${{l}_{1}}$, ${{b}_{1}}$and ${{h}_{1}}$. So from the above diagrams, we have
${{b}_{1}}=l=2cm.$
${{h}_{1}}=l=2cm$
and, \[{{l}_{1}}=l+l+l\]
Now, substituting the values, we get the final dimension as
\[\Rightarrow {{l}_{1}}=3l\]
\[\Rightarrow {{l}_{1}}=3\times 2\]
\[\Rightarrow {{l}_{1}}=6cm\]

So, by joining three cubes, we obtained a cuboid of length $6cm$, breadth $2cm$ and height $2cm$.


Note: This question is pure imagination based question. So students should read very carefully this type of question, and imagine in your mind what the question is trying to ask. There can be extensions of this question, like questions can be asked about the surface area of the cuboid.
And for the surface area of the cuboid, students directly add the surface of three cubes, which is totally wrong. Firstly, we have to calculate the length $l_{1}$ and then apply the formula of surface area.
$l_{1}=3l$
Surface area $S=4l_{1}l+2l^{2}$.