Question

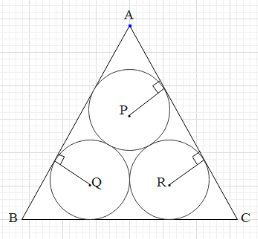
Three circles each of radius r units are drawn inside an equilateral triangle of side ‘a’ units, such that each circle touches the other two and two sides of the triangle as shown in the figure, (P, Q and R are the centres of the three circles). Then the relation between r and a is

A. $a=2\left( \sqrt{3}+1 \right)r$
B. $a=\left( \sqrt{3}+1 \right)r$
C. $a=\left( \sqrt{3}+2 \right)r$
D. $a=2\left( \sqrt{3}+2 \right)r$

Answer 1

Hint:To solve the given question, we must have the knowledge of trigonometry, rules of congruence and properties of a triangle and a rectangle. Divide the given figure into known shapes. Then find the value of one of the sides in terms of the radius of the circle.

Complete step by step answer:
We know that in an equilateral triangle all the sides are of equal lengths and the angles are of ${{60}^{\circ }}$ each. Let us draw some line segments and shown below.

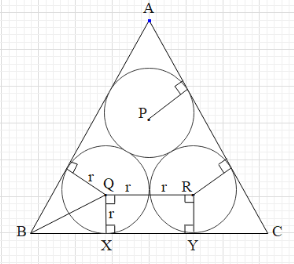
In this, the quadrilateral QRYX is a rectangle since all angles are right angles.
Also we can see that $QR=2r$.
The opposite sides of a rectangle are equal. Then this means that $QR=XY=2r$.
Now consider $\Delta BTQ$ and $\Delta BXQ$. Here,
$TQ=XQ=r$, since they both are the radius of the circle.
$\angle BTQ=\angle BXQ={{90}^{\circ }}$.
And the two triangles have a common side $BQ$.

With this, we get that $\Delta BTQ\cong \Delta BXQ$, by RHS congruence rule.
Now, since $\Delta BTQ\cong \Delta BXQ$, $\angle TBQ=\angle XBQ$.
But $\angle TBQ+\angle XBQ=\angle TBX={{60}^{\circ }}$
Substitute $\angle TBQ=\angle XBQ$.
$\Rightarrow \angle XBQ+\angle XBQ={{60}^{\circ }}$
$\Rightarrow \angle XBQ={{30}^{\circ }}$$\Rightarrow \angle XBQ={{30}^{\circ }}$.
From the knowledge of trigonometry we get that in $\Delta BXQ$, $\tan {{30}^{\circ }}=\dfrac{QX}{BX}=\dfrac{r}{BX}$.

And $\tan {{30}^{\circ }}=\dfrac{1}{\sqrt{3}}$
$\Rightarrow \tan {{30}^{\circ }}=\dfrac{1}{\sqrt{3}}=\dfrac{r}{BX}$
$\Rightarrow BX=\sqrt{3}r$.
Similarly, we will get that $YC=\sqrt{3}r$
And from the figure, $a=BX+XY+YC$ .
Substitute the values of BX, XY and YC.
$\Rightarrow a=\sqrt{3}r+2r+\sqrt{3}r$
$\therefore a=2\left( \sqrt{3}+1 \right)r$

Therefore, we found a relation between a and r. Hence, the correct option is A.

Note: We can see that the given figure has multiple lines of symmetry. Therefore, we do not have to really prove that $\Delta BTQ\cong \Delta BXQ$. Due to symmetry the two triangles will be congruent. Hence, without wasting any time we can write that $\angle TBQ=\angle XBQ$. This will help in competitive exams.