Question

Three children are sitting on a see-saw in such a way that it is balanced. A 20kg and 30kg boy are on opposite sides at a distance of 2m from the pivot. If the third boy jumps off, thereby destroying balance, then the initial angular acceleration of the board is:(Neglect weight of board)
A) $0.01\;rad\,{s^{ - 2}}$
B) $1\;rad\,{s^{ - 2}}$
C) $10\;rad\,{s^{ - 2}}$
D) $100\;rad\,{s^{ - 2}}$

Answer 1

Hint: When a boy jumps off, there will be net torque acting on the system, and two forces at the extreme positions will act and will try to misbalance the system and thereby we can see the effect of net torque acting on the system.

Complete step by step answer:
Refer to the below figure, representing two boys $B_1$ of $30\;{\rm{kg}}$ and $B_2$ of $20\;{\rm{kg}}$and the third boy has jumped off and ${m_1}g$ and ${m_2}g$ are downward forces acting at the positions of the boys $B_1$ and $B_2$.

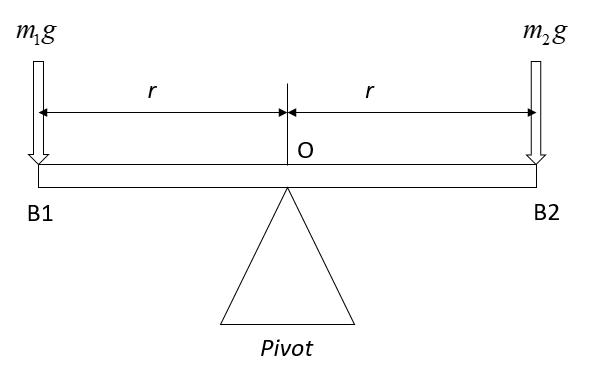
The formula for calculating the angular acceleration is:
$ \Rightarrow \alpha = \dfrac{\tau }{I}$…… (i)
Here, $\alpha $ is the angular acceleration, $\tau $ is the net torque and $I$ is the mass moment of inertia.
Express the relation for calculating net torque at the pivot O.
$ \Rightarrow \tau = {m_1}g \times r - {m_2}g \times r$…… (ii)
Here ${m_1}$ is the mass of $B_1$ and ${m_2}$ is the mass of $B_2 $ and $r$ is the distance of boys from the pivot and $g$ is the acceleration due to gravity.
Substitute${m_1} = 30\;{\rm{kg}}$, ${m_2} = 20\;{\rm{kg}}$ and $r = 2\;{\rm{m}}$in equation (ii) to find the value of net torque.
$ \Rightarrow \tau = 30 \times 10 \times 2 - 20 \times 10 \times 2$
$\therefore \tau = 200\;{\rm{Nm}}$
Express the relation for calculating the moment of inertia about the pivot point.
$I = {m_1} \times {r^2} + {m_2} \times {r^2}$
Substitute ${m_1} = 30\;{\rm{kg}}$, ${m_2} = 20\;{\rm{kg}}$ and $r = 2\;{\rm{m}}$ to find the value of Moment of inertia.
$ \Rightarrow I = 30 \times {2^2} + 20 \times {2^2}$
$\therefore I = 200\;{\rm{kg}}\,{{\rm{m}}^2}$
Substitute $I = 200\;{\rm{kg}}\,{{\rm{m}}^2}$and $\tau = 200\;{\rm{Nm}}$ in equation (i) to find the value of angular acceleration.
$ \Rightarrow \alpha = \dfrac{{200\;{\rm{Nm}}}}{{200\;{\rm{kg}}\,{{\rm{m}}^2}}}$
$\therefore \alpha = 1\;{\rm{rad/}}{{\rm{s}}^{\rm{2}}}$

Therefore the value for initial angular acceleration of the board is $1\;{\rm{rad/}}{{\rm{s}}^{\rm{2}}}$. Hence, Option (B) is correct.

Note:
- When all the three boys were on the board, it was balanced and suddenly when the third boy jumped off, then the board would move in the direction where the torque was high.
- Since the third boy has jumped off suddenly and the system is imbalanced and hence the torque is not going to remain constant and an angular acceleration will act on the whole system which will depend upon the moment of inertia of the whole system.