Question

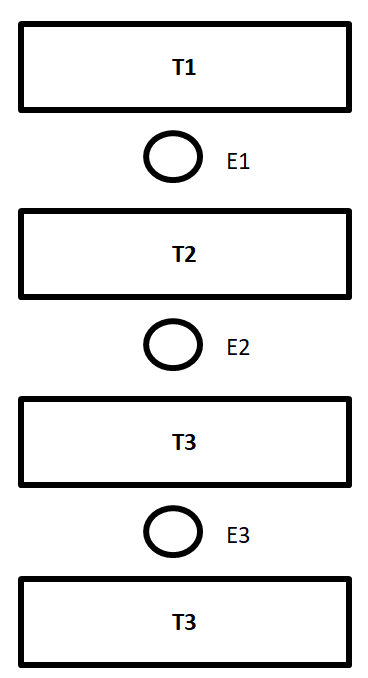
Three Carnot engines operate in series between a heat source at a temperature ${{\text{T}}_1}$ and a heat sink at a temperature ${{\text{T}}_4}$ (see figure). There are two other reservoirs at temperatures ${{\text{T}}_2}$ and ${{\text{T}}_3}$, as shown, with ${{\text{T}}_1} > {{\text{T}}_2} > {{\text{T}}_3} > {{\text{T}}_4}$. The three engines will be equally efficient if

(A) ${{\text{T}}_2} = {\left( {{{\text{T}}_1}^2{{\text{T}}_4}} \right)^{1/3}}$;${{\text{T}}_3} = {\left( {{{\text{T}}_1}{{\text{T}}_4}^2} \right)^{1/3}}$
(B) ${{\text{T}}_2} = {\left( {{{\text{T}}_1}{{\text{T}}_4}^2} \right)^{1/3}}$;${{\text{T}}_3} = {\left( {{{\text{T}}_1}^2{{\text{T}}_4}} \right)^{1/3}}$
(C) ${{\text{T}}_2} = {\left( {{{\text{T}}_1}^3{{\text{T}}_4}} \right)^{1/4}}$;${{\text{T}}_3} = {\left( {{{\text{T}}_1}{{\text{T}}_4}^3} \right)^{1/4}}$
(D) ${{\text{T}}_2} = {\left( {{{\text{T}}_1}{{\text{T}}_4}} \right)^{1/2}}$;${{\text{T}}_3} = {\left( {{{\text{T}}_1}^2{{\text{T}}_4}} \right)^{1/3}}$

Answer 1

Hint To solve this question, we have to use the expression of the efficiency of a heat engine, for the three engines given. Then, we have to equate the three efficiencies to get three equations, with the help of which we will get the answer.
The formula used to solve this question is
$\Rightarrow \eta = 1 - \dfrac{{{T_{sink}}}}{{{T_{source}}}}$, where is the efficiency of a heat engine having ${T_{source}}$ as the temperature of the heat source and ${T_{sink}}$ as the temperature of the heat sink.

Complete step by step answer
Let ${\eta _1}$, ${\eta _2}$ and ${\eta _3}$ be the efficiencies of the heat engines $\Rightarrow {E_1}$,${E_2}$ and ${E_3}$ respectively.
For the heat engine ${E_1}$
As we know that the heat source has a higher temperature than the heat sink.
$\because {{\text{T}}_1} > {{\text{T}}_2}$
So, ${{\text{T}}_1}$ is the temperature of the heat source, and ${{\text{T}}_1}$ is the temperature of the heat sink.
Now, we know that the efficiency of a heat engine is given by
$\Rightarrow \eta = 1 - \dfrac{{{T_{sink}}}}{{{T_{source}}}}$
So, the efficiency of the first heat engine
$\Rightarrow {\eta _1} = 1 - \dfrac{{{T_2}}}{{{T_1}}}$ (1)
Similarly,
$\Rightarrow {\eta _2} = 1 - \dfrac{{{T_3}}}{{{T_4}}}$, and (2)
$\Rightarrow {\eta _3} = 1 - \dfrac{{{T_4}}}{{{T_3}}}$ (3)
According to the question, ${\eta _1} = {\eta _2} = {\eta _3}$
Equating (1) and (2), we get
$\Rightarrow 1 - \dfrac{{{T_2}}}{{{T_1}}} = 1 - \dfrac{{{T_3}}}{{{T_2}}}$
So that
$\Rightarrow \dfrac{{{T_2}}}{{{T_1}}} = \dfrac{{{T_3}}}{{{T_2}}}$
By cross multiplying, we get
$\Rightarrow {T_2}^2 = {T_1}{T_3}$ (4)
Equating (2) and (3), we get
$\Rightarrow 1 - \dfrac{{{T_3}}}{{{T_2}}} = 1 - \dfrac{{{T_4}}}{{{T_3}}}$
So that
$\Rightarrow \dfrac{{{T_3}}}{{{T_2}}} = \dfrac{{{T_4}}}{{{T_3}}}$
By cross multiplying, we get
$\Rightarrow {T_3}^2 = {T_2}{T_4}$ (5)
Equating (1) and (3), we get
$\Rightarrow 1 - \dfrac{{{T_2}}}{{{T_1}}} = 1 - \dfrac{{{T_4}}}{{{T_3}}}$
So that
$\Rightarrow \dfrac{{{T_2}}}{{{T_1}}} = \dfrac{{{T_4}}}{{{T_3}}}$
$\Rightarrow {T_2} = \dfrac{{{T_1}{T_4}}}{{{T_3}}}$ (6)
Dividing (4) by (5)
$\Rightarrow {\left( {\dfrac{{{T_2}}}{{{T_3}}}} \right)^2} = \dfrac{{{T_1}{T_3}}}{{{T_2}{T_4}}}$
Multiplying by $\dfrac{{{T_2}}}{{{T_3}}}$ both the sides
$\Rightarrow {\left( {\dfrac{{{T_2}}}{{{T_3}}}} \right)^3} = \dfrac{{{T_1}}}{{{T_4}}}$
$\Rightarrow \dfrac{{{T_2}}}{{{T_3}}} = {\left( {\dfrac{{{T_1}}}{{{T_4}}}} \right)^{1/3}}$
$\Rightarrow {T_2} = {\left( {\dfrac{{{T_1}}}{{{T_4}}}} \right)^{1/3}}{T_3}$ (7)
Substituting (6)
$\Rightarrow \dfrac{{{T_1}{T_4}}}{{{T_3}}} = {\left( {\dfrac{{{T_1}}}{{{T_4}}}} \right)^{1/3}}{T_3}$
$\Rightarrow {T_3}^2 = {T_1}^{2/3}{T_4}^{4/3}$
Taking square root
$\Rightarrow {T_3} = {T_1}^{1/3}{T_4}^{2/3}$
$\Rightarrow {T_3} = {\left( {{T_1}{T_4}^2} \right)^{1/3}}$
Substituting in (7)
$\Rightarrow {T_2} = {\left( {\dfrac{{{T_1}}}{{{T_4}}}} \right)^{1/3}}{\left( {{T_1}{T_4}^2} \right)^{1/3}}$
$\Rightarrow {T_2} = {T_1}^{2/3}{T_4}^{1/3}$
Or
$\Rightarrow {T_2} = {\left( {{T_1}^2{T_4}} \right)^{1/3}}$
Therefore, ${T_2} = {\left( {{T_1}^2{T_4}} \right)^{1/3}}$and ${T_3} = {\left( {{T_1}{T_4}^2} \right)^{1/3}}$
Hence, the correct answer is option (A).

Note
To solve these types of problems involving multiple variables, we just need to see in the options what variables are to be found out. We just need to separate those variables and write them in the form of remaining variables from the equations formed.