Question

Three capacitors of capacitance $3\mu F$ , $10\mu F$ and $15\mu F$are connected in series to a voltage source of $100mV$ . The charge on $15\mu F$ is
A.$50\mu C$
B.$100\mu C$
D.$200\mu C$
D.$280\mu C$

Answer 1

Hint: Capacitance is the ability of a component or circuit to collect and store energy in form of an electric charge and a capacitor is a device in which we can store the charge. Two or more capacitors in series will have an equal amount of charge across their plates. If the charge is the same and constant, the voltage drop across the capacitor is determined by the value of the capacitor only.
Formula used:
When the capacitor are connected in series
$\dfrac{{\text{1}}}{{{\text{C_eq}}}} = \dfrac{1}{{C_1}} + \dfrac{1}{{C_2}} + \dfrac{1}{{C_3}}$ ………………. (1)
The relation between capacitor and voltage $V = \dfrac{Q}{C}$ ………………. (2)
Where $V$ is a voltage source, $Q$ is charge across the capacitor, $C$ is a capacitor

Complete answer:
In question, it is given that the three capacitors $3\mu F$,$10\mu F$ and $15\mu F$ are connected in series, and from equation (1) $\dfrac{{\text{1}}}{{{\text{C_eq}}}} = \dfrac{1}{{C_1}} + \dfrac{1}{{C_2}} + \dfrac{1}{{C_3}}$

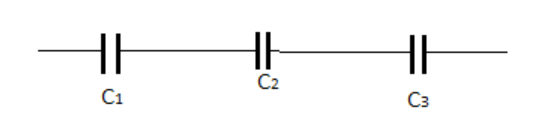
Where $C_1 = 3\mu F$ , $C_2 = 10\mu F$ and $C_3 = 15\mu F$
By putting these values in equation (1)
We get $\dfrac{{\text{1}}}{{{\text{C_eq}}}} = \dfrac{1}{3} + \dfrac{1}{{10}} + \dfrac{1}{{15}}$
$ \Rightarrow \dfrac{{\text{1}}}{{{\text{C_eq}}}} = \dfrac{{10 + 3 + 2}}{{{\text{30}}}}$
$ \Rightarrow \dfrac{{\text{1}}}{{{\text{C_eq}}}} = \dfrac{{15}}{{30}}$
$ \Rightarrow \dfrac{{\text{1}}}{{{\text{C_eq}}}} = \dfrac{1}{2}$
$ \Rightarrow C_eq = 2\mu F$
To find the charge on $15\mu F$, from equation (2)
$Q = C_eqV$ ………. (3)
Given $V = 100mV$
And $C_eq = 2\mu F$
$ \Rightarrow 2\mu F = 2 \times {10^{ - 6}}$
$ \Rightarrow Q = 2 \times {10^{ - 6}} \times 100$
$ \Rightarrow Q = 200\mu C$

So the correct option is (C).

Note:
When the capacitors are connected in series and a voltage is applied across them then the voltage across the capacitor is not equivalent but depends upon the value of the capacitor.
Capacitors in series have different voltages because they do not have the same impedance.
Charge in the capacitor in series is the same and different in a capacitor connected in parallel.
If $C_1$ , $C_2$ and, $C_3$ are connected in parallel then the formula of equivalent capacitance will be:
$C_eq = C_1 + C_2 + C_3$ .