
Three bulbs X, Y and Z are rated as ($p_X$, V), ($p_Y$, V), ($p_Z$, V) respectively. It is given that $p_X > p_Y > p_Z$. Column I indicates the arrangement of the bulbs in different configurations. Column II gives corresponding brightness neglecting the variation in resistance due to change in temperature match the Column I with Column II.
Column I Column II P.
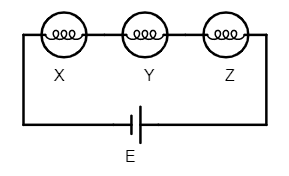
1. Z is glowing with minimum brightness. Q.
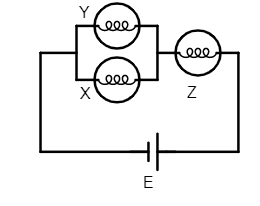
2. X is glowing with minimum brightness. R.
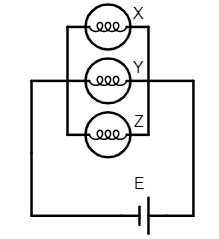
3. Y is glowing with minimum brightness.
| Column I | Column II | ||
| P. | 
| 1. | Z is glowing with minimum brightness. |
| Q. | 
| 2. | X is glowing with minimum brightness. |
| R. | 
| 3. | Y is glowing with minimum brightness. |
Answer
584.1k+ views
Hint: The brightness for the bulbs will be determined by their power consumption. The power consumption will vary depending on the circuit configuration i.e., whether the bulbs are in series or are parallel.
Formula used:
The power consumption of a circuit element is given as:
$P = I^2 R = VI = \dfrac{V^2}{R}$.
Complete answer:
We are given the relation for power rating of 3 bulbs as:
$p_Z < p_Y < p_X$
The power is related to resistance as:
$P = \dfrac{V^2}{R}$
where we already know that V is the same for the three bulbs. As the resistance is inversely proportional to power, the relation for the three resistances is:
$R_Z > R_Y > R_X$
For the three situations in right hand side column of the question, the analysis is done in the following manner:
(i) when the three bulbs are in series combination, the current through all of them will be same given as:
$I = \dfrac{E}{R_X + R_Y + R_Z}$.
$R_X$, $R_Y$ and $R_Z$ are respective resistances of X, Y and Z. We have already seen that resistance of $R_Z$ is the highest and in the formula
$P = I^2 R $,
we can clearly see that power depends on the resistance directly. Therefore, in series connection, bulb X will have minimum brightness among the three bulbs.
(ii) if we consider the case when one of the bulbs is in series and two of the bulbs are parallely connected, then the total current in the circuit is given as:
$I = \dfrac{E}{R_Z + (R_X || R_Y)}$.
Cleary, as we know when we connect two resistances in parallel their equivalent resistance decreases so $R_Z$ will have more potential drop as compared to $R_X || R_Y$ equivalent. When we analyse the parallel circuit, we can see that the current through $R_X$ will be more as we know that current in a parallel circuit always prefers the path of least resistance. Therefore, among the three resistances, $R_Y$ definitely has the least power. So, the match here is- bulb Y has minimum brightness.
(iii) when three bulbs are connected in parallel, current through the three of them will be different but the potential drop across all the three will be the same.
The power consumption is given by
$P = \dfrac{V^2}{R}$.
So, less the resistance, more will be the power and the brightness so, bulb Z will have minimum brightness in this case among the 3 bulbs.
Note:
We are given the power rating for the bulb which is different from the power consumed for an element in a particular circuit. We used different expressions for power for analysis in different cases to find the answer based on resistances only.
Formula used:
The power consumption of a circuit element is given as:
$P = I^2 R = VI = \dfrac{V^2}{R}$.
Complete answer:
We are given the relation for power rating of 3 bulbs as:
$p_Z < p_Y < p_X$
The power is related to resistance as:
$P = \dfrac{V^2}{R}$
where we already know that V is the same for the three bulbs. As the resistance is inversely proportional to power, the relation for the three resistances is:
$R_Z > R_Y > R_X$
For the three situations in right hand side column of the question, the analysis is done in the following manner:
(i) when the three bulbs are in series combination, the current through all of them will be same given as:
$I = \dfrac{E}{R_X + R_Y + R_Z}$.
$R_X$, $R_Y$ and $R_Z$ are respective resistances of X, Y and Z. We have already seen that resistance of $R_Z$ is the highest and in the formula
$P = I^2 R $,
we can clearly see that power depends on the resistance directly. Therefore, in series connection, bulb X will have minimum brightness among the three bulbs.
(ii) if we consider the case when one of the bulbs is in series and two of the bulbs are parallely connected, then the total current in the circuit is given as:
$I = \dfrac{E}{R_Z + (R_X || R_Y)}$.
Cleary, as we know when we connect two resistances in parallel their equivalent resistance decreases so $R_Z$ will have more potential drop as compared to $R_X || R_Y$ equivalent. When we analyse the parallel circuit, we can see that the current through $R_X$ will be more as we know that current in a parallel circuit always prefers the path of least resistance. Therefore, among the three resistances, $R_Y$ definitely has the least power. So, the match here is- bulb Y has minimum brightness.
(iii) when three bulbs are connected in parallel, current through the three of them will be different but the potential drop across all the three will be the same.
The power consumption is given by
$P = \dfrac{V^2}{R}$.
So, less the resistance, more will be the power and the brightness so, bulb Z will have minimum brightness in this case among the 3 bulbs.
Note:
We are given the power rating for the bulb which is different from the power consumed for an element in a particular circuit. We used different expressions for power for analysis in different cases to find the answer based on resistances only.
Recently Updated Pages
Master Class 10 Computer Science: Engaging Questions & Answers for Success

Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Master Class 10 English: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Master Class 10 Science: Engaging Questions & Answers for Success

Trending doubts
What is the median of the first 10 natural numbers class 10 maths CBSE

Which women's tennis player has 24 Grand Slam singles titles?

Who is the Brand Ambassador of Incredible India?

Why is there a time difference of about 5 hours between class 10 social science CBSE

Write a letter to the principal requesting him to grant class 10 english CBSE

A moving boat is observed from the top of a 150 m high class 10 maths CBSE




