Question

Three bells, toll at interval 36 sec, 40 sec, and 48 sec respectively. They start ringing at a particular time. They toll together next after
a)18 minutes
b)12 minutes
c)6 minutes
d)24 minutes

Answer 1

Hint: As in the question, it is asked at what time will all the balls toll together one should try to get LCM of all the time intervals to get the desired result.

Complete step-by-step answer:

We have been given three bells that commence tolling together and toll at intervals of 36, 40, and 48 seconds respectively.

Now, we are asked to find at a time will the all the bells toll together.

We will get the time at which all will toll together is by taking L.C.M or least common multiple all the six-time intervals.

At first, we will know what is LCM or the least common multiple and how to find it.

In arithmetic, the least common multiple, lowest common multiple or smallest common multiple of two integers a and b which is denoted by LCM $\left( a,b \right)$ is the smallest possible integer that is divisible by both a and b. Since the division of integers by zero is undefined, this definition has meaning only if a and b are both different from zero.

If there are more than two numbers, then L.C.M can be done by division method. The numbers will be operated simultaneously. The factors in the division method should divide the minimum of two numbers and it should be until the last term becomes 1 or a prime number to be divided.

Let’s take L.C.M of three bell’s time intervals which are 36, 40, and 48.

So, it can be represented as,

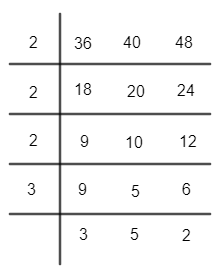
Now for finding the L.C.M we will multiply the divisors and the prime numbers which are left behind.
So, least common multiple $=2\times 2\times 2\times 3\times 3\times 5\times 2$
$=720$
Hence, the least common multiple is 720 sec.
So, all the bells will toll at 720 sec or 12 minutes.
Option ‘b’ is the correct answer.

Note: Students while dealing with application-related HCF, LCM problems they generally confuse themselves by which to choose and how to do it. So, they have to practice with this kind of problem to prevent confusion.