
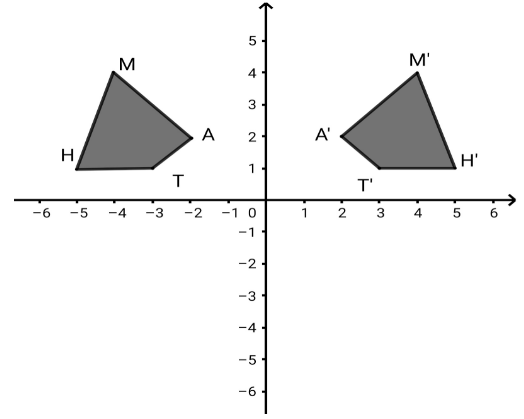
This graph illustrates a reflection over the x-axis. State true and false.
A. True
B. False

Answer
508.5k+ views
Hint: In this question, we have to tell whether the given graph represents reflection about the x-axis or not. We will use the fact that a graph is reflected about x-axis, then it looks symmetric about x-axis and its x-coordinates change it’s sign. Therefore we proceed by listing the coordinates of the vertices of the graph on the left of the y-axis and comparing them with the coordinates of the point on the right side of the y-axis . After comparing we will find that it is not reflected about the x-axis.
Complete step by step answer:
Consider the given question, we are given a graph,
From the graph, we find the coordinates of the vertices of the given polygon.
The vertices of the polygon on left side of y-axis are \[T\left( { - 3,{\text{ }}1} \right)\], \[H\left( { - 5,{\text{ }}1} \right)\], \[A\left( { - 2,{\text{ }}2} \right)\] and \[M\left( { - 4,{\text{ }}4} \right)\].
The vertices of the polygon on right side of y-axis are \[T'\left( {3,{\text{ }}1} \right)\], \[H'\left( {5,{\text{ }}1} \right)\], \[A'\left( {2,2} \right)\;\] and \[M'\left( {4,{\text{ }}4} \right)\].
We know that if the graph is a reflection over the x-axis, then it looks symmetric about the x- axis . Also, the coordinates of the point \[A(x,y)\] changes to \[{A^1}(x, - y)\]. i.e. (\[y\] coordinates changes its sign). Also, if the graph is reflected over the y-axis, then it looks symmetric about the y-axis. also the coordinate of the point \[A(x,y)\] changes to \[{A^1}( - x,y)\]. i.e. (\[x\] coordinates change its sign).
Therefore, comparing the coordinates of \[T\left( { - 3,{\text{ }}1} \right)\] and \[T'\left( {3,{\text{ }}1} \right)\], \[H\left( { - 5,{\text{ }}1} \right)\] and \[H'\left( {5,{\text{ }}1} \right)\],\[A\left( { - 2,{\text{ }}2} \right)\]and \[A'\left( {2,2} \right)\;\], \[M\left( { - 4,{\text{ }}4} \right)\] and \[M'\left( {4,{\text{ }}4} \right)\], we find that its \[x\]-coordinate changes its sign. \[A(x,y)\] changes to \[{A^1}( - x,y)\]. i.e. (\[x\] coordinates change its sign).Therefore, the given coordinates of points from the graph are reflected about the y-axis. Hence, the graph does not reflect over the x-axis.
Therefore, option B is the correct answer.
Note: We first list the coordinates of \[x\] and then the coordinates of \[y\] from the graph. This coordinate is enclosed in bracket, i.e. \[A(x,y)\]. If the graph is a reflection over the x-axis, then it looks symmetric about the x- axis . Also the coordinates of the point \[A(x,y)\] changes to \[{A^1}(x, - y)\]. i.e. (\[y\] coordinates changes its sign). If the graph is reflected over the y-axis, then it looks symmetric about the y-axis . Also the coordinate of the point \[A(x,y)\] changes to \[{A^1}( - x,y)\]. i.e. (\[x\] coordinates change its sign).
Complete step by step answer:
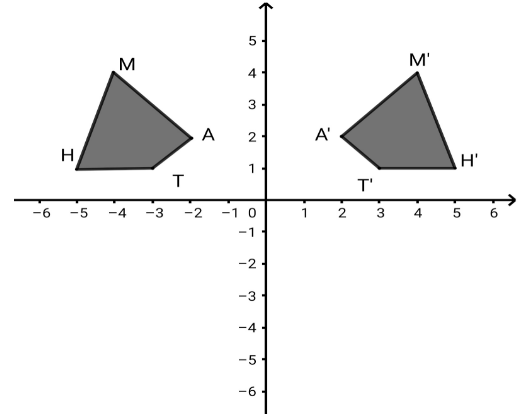
Consider the given question, we are given a graph,

From the graph, we find the coordinates of the vertices of the given polygon.
The vertices of the polygon on left side of y-axis are \[T\left( { - 3,{\text{ }}1} \right)\], \[H\left( { - 5,{\text{ }}1} \right)\], \[A\left( { - 2,{\text{ }}2} \right)\] and \[M\left( { - 4,{\text{ }}4} \right)\].
The vertices of the polygon on right side of y-axis are \[T'\left( {3,{\text{ }}1} \right)\], \[H'\left( {5,{\text{ }}1} \right)\], \[A'\left( {2,2} \right)\;\] and \[M'\left( {4,{\text{ }}4} \right)\].
We know that if the graph is a reflection over the x-axis, then it looks symmetric about the x- axis . Also, the coordinates of the point \[A(x,y)\] changes to \[{A^1}(x, - y)\]. i.e. (\[y\] coordinates changes its sign). Also, if the graph is reflected over the y-axis, then it looks symmetric about the y-axis. also the coordinate of the point \[A(x,y)\] changes to \[{A^1}( - x,y)\]. i.e. (\[x\] coordinates change its sign).
Therefore, comparing the coordinates of \[T\left( { - 3,{\text{ }}1} \right)\] and \[T'\left( {3,{\text{ }}1} \right)\], \[H\left( { - 5,{\text{ }}1} \right)\] and \[H'\left( {5,{\text{ }}1} \right)\],\[A\left( { - 2,{\text{ }}2} \right)\]and \[A'\left( {2,2} \right)\;\], \[M\left( { - 4,{\text{ }}4} \right)\] and \[M'\left( {4,{\text{ }}4} \right)\], we find that its \[x\]-coordinate changes its sign. \[A(x,y)\] changes to \[{A^1}( - x,y)\]. i.e. (\[x\] coordinates change its sign).Therefore, the given coordinates of points from the graph are reflected about the y-axis. Hence, the graph does not reflect over the x-axis.
Therefore, option B is the correct answer.
Note: We first list the coordinates of \[x\] and then the coordinates of \[y\] from the graph. This coordinate is enclosed in bracket, i.e. \[A(x,y)\]. If the graph is a reflection over the x-axis, then it looks symmetric about the x- axis . Also the coordinates of the point \[A(x,y)\] changes to \[{A^1}(x, - y)\]. i.e. (\[y\] coordinates changes its sign). If the graph is reflected over the y-axis, then it looks symmetric about the y-axis . Also the coordinate of the point \[A(x,y)\] changes to \[{A^1}( - x,y)\]. i.e. (\[x\] coordinates change its sign).
Recently Updated Pages
Master Class 8 Social Science: Engaging Questions & Answers for Success

Master Class 8 English: Engaging Questions & Answers for Success

Class 8 Question and Answer - Your Ultimate Solutions Guide

Master Class 8 Maths: Engaging Questions & Answers for Success

Master Class 8 Science: Engaging Questions & Answers for Success

Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Trending doubts
What is BLO What is the full form of BLO class 8 social science CBSE

Citizens of India can vote at the age of A 18 years class 8 social science CBSE

Full form of STD, ISD and PCO

Advantages and disadvantages of science

Right to vote is a AFundamental Right BFundamental class 8 social science CBSE

What are the 12 elements of nature class 8 chemistry CBSE





