Question

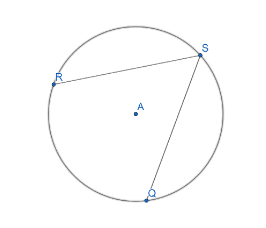
This figure shows circle A with inscribed $ \angle RSQ. $ m $ \angle RSQ = {24^ \circ } $ what is the measure of RSQ?

Answer 1

Hint: The given question of geometry asks us to find the arc angle of the $ RSQ $ . First we will have to remember this conjecture about the inscribed angle , The conjecture goes as follows,
The inscribed angle is one half the arc it cuts. The converse is also true; an arc is double the measure of the angle by which is cut. This given conjecture or theorem means that the inscribed angle is always one half the arc angle it cuts. Thus we will use this conjecture to get the value of the arc angle $ RSQ $ .
We will first get value of arc angle
 $ \widehat {RQ} $
Then use the point that
 $ \widehat {RSQ} + \widehat {RQ} = {360^0} $
To get the value of $ \widehat {RSQ} $.

Complete step by step solution:
First we will write the conjecture that will help us prove this question, the conjecture is about the inscribed angles in a circle. The inscribed angle is one half the arc it cuts. The converse is also true; an arc is double the measure of the angle by which is cut. This given conjecture or theorem means that the inscribed angle is always one half the arc angle it cuts. Thus we will use this conjecture to get the value of the arc angle $ RSQ $ .
We now write,
 $ \widehat {RQ} = 2 \cdot m\angle RQ $
 $ 2 \cdot m\angle RQ = 2 \cdot 24 $
 $ \widehat {RQ} = {48^0} $
Now since we know that a circle must be $ 360 $ degrees.
We will write,
 $ \widehat {RSQ} + {48^0} = {360^0} $
 $ \widehat {RSQ} = {312^0} $
Which is our final answer.
So, the correct answer is “ $ \widehat {RSQ} = {312^0} $ ”.

Note: Remember this conjecture,
The inscribed angle is one half the arc it cuts. The converse is also true; an arc is double the measure of the angle by which is cut. This given conjecture or theorem means that the inscribed angle is always one half the arc angle it cuts