Question

These questions are based on the following pre-chart
Arun’s monthly income is Rs $21,000$
If the rent is increased by ${\text{5% }}$ and the other expenditure and income are the same. So then by what percent does saving decrease?
 

${\text{a)60% }}$
${\text{b)75% }}$
 ${\text{c)25% }}$
${\text{d)40% }}$

Answer 1

Hint: First, we have to find the original saving percentage by subtracting all the other expenses.
Then, we have to increase the rent by ${\text{5% }}$ and find a new saving percentage.
With that, we will have to apply a formula to find the decreased percentage of savings.

Formula used: Change in percentage $ = \dfrac{{{\text{old value - new value}}}}{{{\text{old value}}}} \times 100$

Complete step-by-step solution:
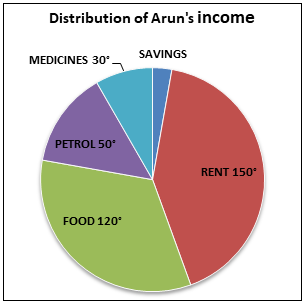
It is given that the pie chart stated as,
Rent = ${\text{150}}^\circ $
Food = ${\text{120}}^\circ $
Petrol = ${\text{50}}^\circ $
Medicines = ${\text{30}}^\circ $
Here, we will find the original old savings percentage.
As we know, the full circle is ${\text{360}}^\circ $ and savings percentage is one among the ${\text{360}}^\circ $
So we can write it as,
Old Savings = ${\text{360}}^\circ - $ rent – food – petrol – medicines.
On putting the values and we get
$ \Rightarrow 360^\circ - 150^\circ - 120^\circ - 50^\circ - 30^\circ $
On simplifying we get
Old savings $ = 10^\circ $
Now, it is given that the rent is increased by ${\text{5% }}$
We have to find the increased percentage of rent,
Old rent = ${\text{150}}^\circ $
Increased percent = ${\text{5% }}$
$\therefore $Increased rent percent = $150 \times \dfrac{5}{{100}}$
$ \Rightarrow \dfrac{{750}}{{100}}$
On dividing we get,
$ \Rightarrow 7.5^\circ $
So the new rent = ${\text{150}}^\circ + 7.5^\circ = 157.5^\circ $
Now we have to find out the new savings = ${\text{360}}^\circ - $ new rent – food – petrol – medicines.
$ \Rightarrow 360^\circ - 157.5^\circ - 120^\circ - 50^\circ - 30^\circ $
On simplifying we get
New savings $ = 2.5^\circ $
Now, we have both the old and new savings, from this we will find the decreased percent of savings.
Change in percentage $ = \dfrac{{{\text{old value - new value}}}}{{{\text{old value}}}} \times 100$
Putting the values and we get
$\therefore $ Decreased savings percent $ = \dfrac{{{\text{10 - 2}}{\text{.5}}}}{{{\text{10}}}} \times 100$
Let us subtract the numerator term and we get,
$ \Rightarrow \dfrac{{7.5}}{{10}} \times 100$
Let us multiply the terms and we get
$ = \dfrac{{750}}{{10}} = 75% $
Therefore, the savings percent is decreased by $75% $

Hence the correct option is $\left( B \right)$.

Note: Basically when we convert numbers into percentages or any data into percentages, nature will change, numbers have no end but percentage does have an end (e.g. ${\text{100% }}$).
When we simply subtract or add the changes, the base (or end) will change (e.g. ${\text{100% }}$ will change either below ${\text{100% }}$ or above ${\text{100% }}$).